Величины в заданный интервал.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, в) , равна определённому интервалу от дифференциальной функции, взятому в пределах от а до в

.

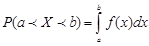Геометрически это можно истолковать так: Р(а < Х < в) численно равна площади криволинейной трапеции, ограниченной линиями:

х=а, х=в, у=0, у= ƒ(х).

 

 

 

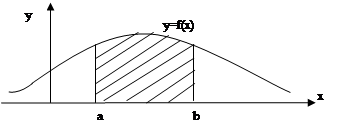
Замечание: если ѓ(х) чётная, концы интервала симметричны относительно начала координат, то

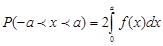
Зная дифференциальную функцию, можно найти интегральную функцию распределения вероятностей по формуле:

.
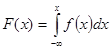