Алгоритм моделирования по принципу Dt.
Укрупнённая схема моделирующего алгоритма, который реализует принцип постоянного приращения модельного времени (принципа Dt), представлен на следующем рисунке:
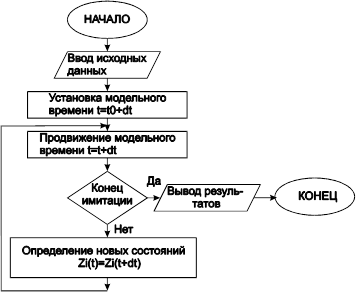
Рис. 5.2. Обобщённый алгоритм моделирования систем по принципу приращений "Dt"
В начале инициализируется программа, в частности вводятся значения Zi(t0), i=1,2,…k. Которые характеризуют состояние системы в k-мерном фазовом пространстве состояний в начальный момент времени t0. Модельное время устанавливается t = t0= 0. Основные операции по имитации системы осуществляется в цикле. Функционирование системы отслеживается по последовательной схеме состояний Zi(t). Для этого модельному даётся некоторое приращение dt. Затем по вектору текущих состояний определяются новые состояния Zi(t + dt), которые становятся текущими. Для определения новых состояний по текущим в формализованном описании системы должны существовать необходимые математические зависимости. По ходу имитации измеряются, вычисляются, фиксируются необходимые выходные характеристики. При моделировании стохастических систем вместо новых состояний вычисляются распределения вероятностей для возможных состояний. Конкретные значения вектора текущих состояний определяются по результатам случайных испытаний. В результате проведения имитационного эксперимента получается одна из возможных реализаций случайного многомерного процесса в заданном интервале времени (t0 , Tk).
Моделирующий алгоритм, основанный на применении dt применим для более широкого круга систем, чем алгоритм, построенный по принципу особых состояний. Однако при его реализации возникают проблемы определения величины dt. Для моделирования ВС на системном уровне в основном используются принцип особых состояний.