Общая постановка задачи линейного программирования

Во всех рассмотренных примерах целевая функция являлась линейной функцией переменных задачи, а все ограничения имели вид линейных равенств и/или неравенств. Учитывая сказанное, в общем виде задачу линейного программирования можно сформулировать следующим образом: найти экстремум (максимум или минимум) целевой функции

при ограничениях

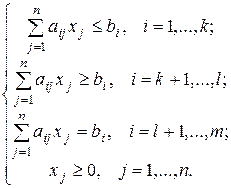
Оптимальным решением (или оптимальным планом) задачи ЛП называется решение Х = (х₁, х₂, …, х_п), удовлетворяющее указанным ограничениям, при котором целевая функция принимает оптимальное (максимальное или минимальное) значение.

Термины «решение» и «план» – синонимы, однако первый используется чаще, когда речь идет о формальной стороне задачи (ее математическом решении), а второй – о содержательной стороне (экономической интерпретации).

Если система ограничений содержит только неравенства, то ЗЛП называется стандартной, если только равенства – канонической.

Любая задача линейного программирования может быть сведена к каноническому виду. Для этого во все ограничения-неравенства необходимо ввести дополнительные переменные x_n+i, положив:

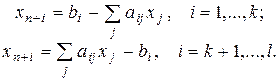
Можно показать, что общая задача ЛП имеет решение тогда и только тогда, когда соответствующая ей каноническая ЗЛП имеет решение.