Магнитный поток

 

Магнитное поле, как и любое векторное может быть наглядно представлено с помощью силовых линий магнитного поля.

Густота силовых линий прямо пропорциональна модулю вектора индукции. Если в неоднородное магнитное поле поместить площадку dS, в пределах которой магнитное поле считается однородн ым, то силовые линии пронизывают ее. В этом случае площадку dS пронизывает магнитный поток (рис. 5): (19)

Рис. 5

или 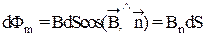. (20)

Полный магнитный поток сквозь произвольную поверхность найдем интегрированием (6.19):

. (21)

Если магнитное поле однородно, то магнитный поток

Ф_m= ВScosa. (22)

При a = 90^о Ф_m= 0. В этом случае силовые линии магнитного поля скользят вдоль поверхности, не пересекая ее. При a = 0^о магнитный поток максимален, Ф_m = ВS. В СИ магнитный поток измеряется в веберах (Вб).

Рис. 6

Магнитный поток пронизывающий произвольную замкнутую поверхность, равен нулю (теорема Гаусса для вектора ).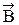

В качестве примера рассмотрим магнитное поле прямого тока. Окружим проводник с током цилиндрической поверхностью произвольного радиуса основания r (рис. 6). Силовые линии магнитного поля прямого тока представляют собой концентрические окружности с центром на оси проводника. В данном случае силовые линии не пересекают цилиндрическую поверхность, поэтому магнитный поток сквозь ее, равен нулю, т. е. = 0. (23)

Вывод: Число силовых линий, выходящих из замкнутой поверхности, равно числу линий, входящих в область, ограниченную этой поверхностью, и не зависит от формы и размеров ее. Из данной теоремы следует, что в природе не существуют магнитные заряды. Однако теория «Великого Объединения» допускает существование магнитных зарядов - магнитных монополей Дирака. Согласно квантовой теории магнитный поток квантуется.

Для расширения возможности применения теоремы Гаусса для вектора 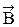формулу (24) записывают в дифференциальной форме:

div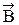= 0 или = 0, (24)