Integer (алгоритм Брезенхема, 1965 г.)

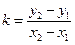, где y₂–y₁ – целое, и x₂–x₁ – то же целое.

Поскольку d вычисляется как конечная сумма элементов, каждый из которых равен либо k, либо –1, то d является также рациональной дробью и k может быть записана в виде частного со знаменателем (x₂–x₁). Для избавления от нецелого 0.5 необходимо умножить знаменатель на 2. Теперь

V=2*(x2-x1)

K=k*V

D=d*V

Условие изменится так: d>0.5 => d*v>0.5*v => D>(x2-x1) => D>dx .

Т.к. сравнение с нулем производится быстрее, то D-dx>dx => D-dx => E>0,

где E=D-dx. Т.к. первоначально d=0, то и D=0 => первоначально E=-dx

dx=x2-x1;

dy=y2-y1;

V=dx*2;

K=dy*2;

E=-dx;

y=y1;

for (x=x1; x<=x2;x++) {

point(x, y);

E+=K;

if (E>0) {y++; E-=V;}

}

Если расстояние по вертикали между T₁ и T₂ больше, чем по горизонтали, то независимой переменной будет y вместо x.