Построение общего решения.

 

Знание ФСР даёт возможность построения общего решения системы (2).

 

Основная теорема:

Если 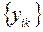, , 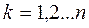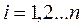есть фундаментальная система решений в интервале 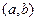, то формулы 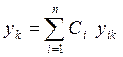, 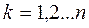(22), где

произвольные постоянные, дают общее решение системы в области , , .

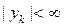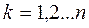Действительно, система (22) разрешима относительно 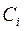, так как , кроме этого совокупность функций (22) является решением системы (2), что соответствует определению общего решения нормальной системы дифференциальных уравнений. Чтобы найти частное решение, удовлетворяющее условиям 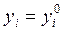при нужно подставить эти условия в систему (22).

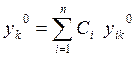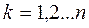, (230

находим , откуда следует, что 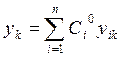, 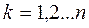(24) – есть искомое решение.