Фундаментальная система решений.

 

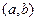Совокупность решений однородной системы (2), определенный и линейно независимыми в интервале , называется фундаментальной системой решений в интервале .

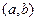Кратко, 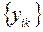, , 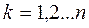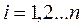(19).

Теорема:

Система (2) всегда имеет ФСР в области непрерывности коэффициентов системы.

Возьмём 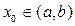и построим решений

,

,

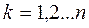
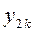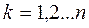
… (20)

,

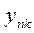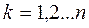
со следующими начальными условиями:

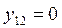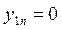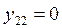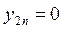, ,…,, при

, ,…,, при

…… (21)

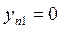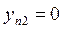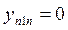, ,…,, при

 

Вронскиан решений (20) в точке 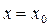равен единице.

Следовательно, совокупность решений (20) линейно независима и является ФСР.

Из доказательства теоремы следует, что фундаментальных систем существует бесконечное множество. Построенная фундаментальная система (21) называется нормированной в точке 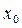. Для каждой точки 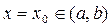существует только одна нормированная в этой точке ФСР.