Точные методы решения

В курсе уравнений математической физики[2] изложен ряд методов нахождения точных решений. К ним относятся метод распространения волн, метод разделения переменных, метод функции Грина или источника.

Например, для простейшей задачи теплопроводности:

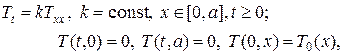(8)

методом разделения переменных можно найти точное решение в виде бесконечной суммы

(9)

где соответствующие коэффициенты Фурье от начальных данных находятся в соответствии с формулой

. (10)

Решение задачи (8) — (10) проиллюстрируем на конкретном примере, код программы для которого приведен на листинге_№1.

 

Листинг_№1

%Изображение аналитического решения уравнения

%теплопроводности, представленного в виде

%конечного отрезка бесконечного ряда

%очищаем рабочее пространство

clear all

%определяем коэффициент теплопроводности и

%длину отрезка интегрирования

k=1; a=1;

%определяем константы начального распределения

%температуры T0(x)=px, 0<=x<=0.5a; T0(x)=q(a-x),

%0.5a<x<=a

q=1; p=2;

%определяем число учтенных слагаемых

%бесконечного ряда

N=40;

%вычисляем первые N коэффициентов Фурье от

%начального распределения

for n=1:N

alpha(n)=((a*(q-p))/(pi*n))*cos(0.5*pi*n)+...

((2*a*(q+p))/(pi^2*n^2))*sin(0.5*pi*n);

end

%определяем сетки по времени и по пространству,

%в точках которых будет найдено значение температуры

t=0:0.05:10;

x=0:0.01:a;

%строим начальный температурный профиль T0

for j=1:length(x)

if x(j)<=0.5*a

T(j)=p*x(j);

end

if x(j)>0.5*a

T(j)=q*(a-x(j));

end

end

%рисуем начальный температурный профиль

plot(x,T,'Color','red','LineWidth',3);

hold on

%организуем цикл вычисления значений температуры

%в различные моменты времени и изображение их на

%едином графике

for i=1:length(t)

for j=1:length(x)

s=0;

for n=1:N

s=s+alpha(n)*...

exp(-(pi^2*n^2*k*t(i))/a^2)*...

sin((pi*n*x(j))/a);

end

T(j)=s;

end

plot(x,T);

hold on

end

 

На рис.1 приведен итог работы кода программы листинга_№1. Из графика видно, как начальные неоднородности, намеренно выбранные в виде острого кусочно-непрерывного профиля, со временем становятся гладкими линиями.

Подставляя (10) в (9) и меняя местами знаки интегрирование и суммирования, находим выражение для решения исходной задачи в терминах функции Грина

, (11)

где функция источника (Грина) равна

. (12)

 

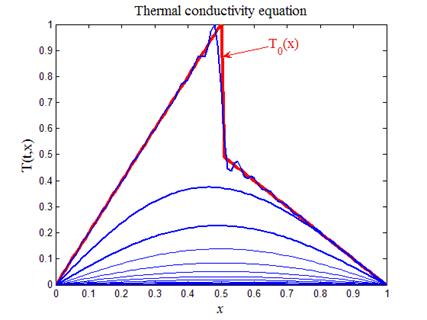
Рис.1. Решение задачи (8) — (10)

 

Функция Грина для задачи Коши на всей оси имеет наиболее простой вид

. (12¢)

Функции влияния, подобные (12), (12¢) позволяют связать начальные данные с решением и сделать ряд важных замечаний о решениях в целом. Так, если начальное распределение сосредоточено на некотором отрезке [a,b], т.е. T₀(x) > 0 при x Î [a,b] и T₀(x) = 0, когда x Ï [a,b], то, согласно (11), (12¢), при t > 0 решение будет отличным от нуля в любой точке бесконечной оси. Это можно истолковать как то, что скорость распространения тепла в уравнении с линейной теплопроводностью бесконечна. Для сравнения с нелинейной теплопроводностью сошлемся на модель №5 в лекции №1. В этой модели рассматривалась ситуация остановки на некоторое время фронта тепловой волны.