Уравнение Ленгмюра

Зависимость величины адсорбции от давления (для газов) или концентрации (для растворов) дается уравнением Ленгмюра. Обозначим:

x – число центров адсорбции на единице поверхности;

y – число занятых центров адсорбции на той же поверхности;

Рис. 2. Свободные и занятые центры адсорбции на поверхности адсорбента.

Скорость адсорбции пропорциональна числу свободных центров

v_a = k_a(x–y)p

Скорость десорбции пропорциональна числу занятых центров

v_d = k_dy

В состоянии равновесия

v_a = v_d или

k_dy = k_a(x–y)p

Адсорбция равна отношению числа центров к числу Авогадро:

k_dа = k_a(а_∞–а)p

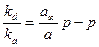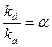; ; α – константа адсорбционного равновесия;

После подстановки α и преобразования получаем

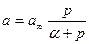– уравнение Ленгмюра

Рис. 3. Изотерма адсорбции

Для определения постоянных этого уравнения, то есть предельной адсорбции а_¥ и константы адсорбционного равновесия α переменные величины – адсорбцию и давление (концентрацию в случае адсорбции из растворов) – преобразуют в обратные им значения:

График в координатах 1/р (1/с) – 1/а оказывается прямой линией, что облегчает определение постоянных адсорбции.

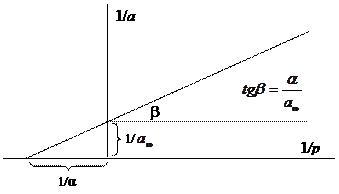
Рис 4. Графическое определение постоянных адсорбции

Нередко применяется также уравнение изотермы Фрейндлиха

a = k∙pⁿ

где a – количество адсорбированного вещества, – константа, численно равная адсорбции при равновесном давлении газа 101,3 кПа (1 атм), моль/(кг∙кПа); р – давление газа, кПа; n – константа, определяющая кривизну изотермы адсорбции, ее значение колеблется в пределах от 0,1 – 0,6.