Анализ времени работы сортировки слиянием через рекуррентное соотношение

 

Для простоты будем предполагать, что размер массива есть степень двойки. Тогда на каждом шаге сортируемый участок делится на две равные половины. Разбиение на части (вычисление границы) требует времени Θ(1), а слияние – времени Θ(n). Получаем соотношение

 

 

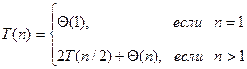
Это соотношение влечёт T(n) = Θ(n×log n), где через log обозначается двоичный логарифм (основание логарифмов, впрочем, не играет роли, так как приводит лишь к изменению константы). Поэтому для больших n сортировка слиянием эффективнее сортировки вставками, требующей времени Q(n²).