Свойства функций, непрерывных на отрезке.

Теорема 1. Функция, непрерывная на отрезке, принимает хотя бы в одной точке отрезка наибольшее значение и хотя бы в одной наименьшее. (Разумеется таких точек несколько).

Это утверждение становится неверным, если отрезок заменить интервалом ( или )

Пример.

То же и для разрывных функций.

Теорема 2. Функция, непрерывная на отрезке и принимающая на концах отрезка значения разных знаков, хотя бы один раз обращается в нуль внутри отрезка.

Геометрически это очевидно функция обязательно пересечет ось .

Для разрывных функций утверждение не проходит.

Теорема 3. Является обобщением теоремы 2.

Пусть 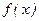определена непрерывна на . Если на концах отрезка функция принимает неравные значения и , то каково бы ни было число , заключенное между и , найдется такая точка , что .

Следствие теоремы 3. Если 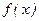непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает по крайней мере один раз любое значение, заключенное между наибольшим и наименьшим.