Дискретно-непрерывная система Глушкова.

Модели Глушкова применяются для моделирования непрерывно-дискретных систем. Формализм описания включает в себя математическую модель непрерывно-дискретной системы, язык спецификации, а также набор процедур и функций реализации моделирующего алгоритма. В противоположность агрегативному подходу, моделирующий алгоритм В.М.Глушкова базируется на дискретном событийном подходе к моделированию сложных систем.

Непрерывно-дискретной системой называется математическая модель вида:

, (8.2)

где - дискретная модель времени;

-- множество классов процессов:

-- множество классов событий (причин мгновенной смены поведения и структуры системы);

-- множество алгоритмов классов событий (подготовительных дискретных действий при переходе к новому поведению системы);

- календарь планирования событий;

-- список уравнений, характеризующих локальные поведения процессов во временных интервалах между событиями.

В календарь планирования событий записываются отметки о событиях отдельными объектами, с его помощью описывается динамика системы. Планирование события подразумевает явное задание момента его наступления или задание условия его наступления. Модель календаря можно представить видом:

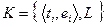, (8.3)

где - условие его наступления (планирование события по условию, задается предикатом).

Структура процесса и его поведение описывается математической моделью:

, (8.4)

где , -- каналы входа и выхода;

- множество статических переменных процесса, которые задаются алгебраическими выражениями и могут меняться только при исполнении алгоритмов событий;

- множество "переменных-функций" - динамических переменных, которые задаются дифференциальными уравнениями из множества ;

- тело процесса, содержащее описания его всевозможных повелений.

Под моделированием поведения непрерывно-дискретной системы понимается построение множества последовательностей событий, приводящих к смене ее поведения и структуры, причисляя к событию начальное состояние системы. Глобальное поведение моделируется с помощью специального процесса-монитора, который продвигает системное время в соответствии с календарем планирования событий или в соответствии с анализом времени наступления события, которое планируется по условию. Процесс моделирования заканчивается, когда календарь событий оказывается пустым.

Модели Бусленко и Глушкова используют разные подходы к описанию одного и того же класса сложных систем. Во всех подходах предлагаемые модели рассматриваются как расширение базовой (непрерывной или дискретной) модели, поэтому поведение непрерывно-дискретной системы представляется в них с разных точек зрения и с разными, иногда противоположными, акцентами.

Для моделирования систем Глушкова разработана система моделирования НЕДИС.