Вычисление объемов тел вращения.
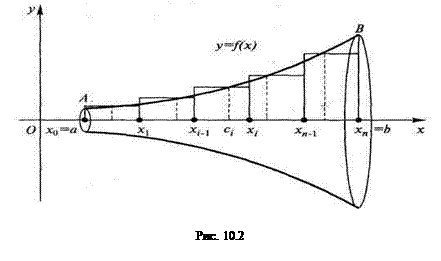 |
Рассмотрим тело, образованное вращением вокруг оси
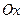 криволинейной трапеции
криволинейной трапеции  , ограниченной графиком неотрицательной непрерывной функции
, ограниченной графиком неотрицательной непрерывной функции 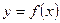 ,
,  ,осью абсцисс и отрезками прямых
,осью абсцисс и отрезками прямых  (рис. 10.2).
(рис. 10.2).
| |
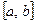 точками
точками 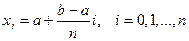 на
на  частей равной длины. На каждом из отрезков
частей равной длины. На каждом из отрезков 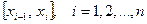 , выберем некоторую точку
, выберем некоторую точку 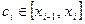 и составим интегральную сумму:
и составим интегральную сумму:
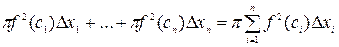 , (10.6)
, (10.6)
где 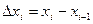 . Каждый член полученной суммы равен объему кругового цилиндра, а вся сумма равна объему соответствующего ступенчатого тела. Для непрерывной функции
. Каждый член полученной суммы равен объему кругового цилиндра, а вся сумма равна объему соответствующего ступенчатого тела. Для непрерывной функции 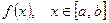 ,предел интегральных сумм (10.6) при n→∞ существует и равен объему V рассматриваемого тела вращения:
,предел интегральных сумм (10.6) при n→∞ существует и равен объему V рассматриваемого тела вращения:
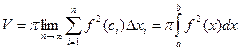 .
.