Радиус произвольного нормального сечения. Средний радиус кривизны поверхности эллипсоида.

Кривизна поверхности эллипсоида в произвольном направлении определяется кривизной нормального сечения, проходящего в азимуте А и выражается уравнением Эйлера в функции главных радиусов кривизны

 

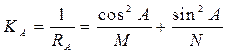, ( 4. 16 )

 

откуда несложно получить выражение для радиуса кривизны произвольного нормального сечения

( 4. 17 )

 

Данное выражение получим после несложных преобразований в виде

, ( 4. 18 )

где h2 = e/2 cos2 B. Это обозначение принято в высшей геодезии и будет использовано нами дальше.

Для решения целого ряда практических задач геодезии на территориях малых размеров с целью упрощения рабочих формул для вычислений поверхность эллипсоида заменяют поверхностью шара, радиус которого принимается равным среднему интегральному значению радиусов кривизны эллипсоида в данной точке. Некоторые из этих задач мы будем рассматривать дальше. Естественно, при этом важным является вопрос расчета точности вычислений.

Среднее интегральное значение для выражения ( 4. 17 ) в точке будет зависеть только от азимута. При этом видно из выражения ( 4. 17 ), что эта зависимость одинакова в четырех квадрантах, поэтому можем записать

 

. ( 4. 19 )

 

Подставляя выражение ( 4. 17 ) в ( 4. 18 ), разделим числитель и знаменатель подынтегральной функции на Ncos2 A , в результате запишем

( 4. 20 )

Для приведения полученного выражения к табличному интегралу введем новую переменную по формуле

 

,

 

В результате имеем выражение, взамен ( 4. 19 )

 

( 4. 21 )

Как видим, средний радиус кривизны поверхности эллипсоида равен среднему геометрическому из главных радиусов кривизны. Подставляя в полученное выражение значения главных радиусов кривизны, имеем

 

( 4. 22 )

 

Полезно запомнить выражения для радиусов кривизны, если используется полярный радиус кривизны ( 4. 13 ) и вторая функция широты ( 4. 9 ).

( 4. 23 )

Вторую функцию широты можно также выразить через второй эксцентриситет в виде

( 4. 24 )

Средний радиус кривизны эллипсоида применяется для упрощения решения целого ряда геодезических задач: решении треугольников, редукционной проблемы, а также в картографии.