Сжатие изображений на основе вейвлетной фильтрации
Выше рассматривалось кодирование изображений с помощью разложения по гармоническим функциям. Возможное усовершенствование такого подхода состоит в выборе другой системы функций, обеспечивающей лучшую локализацию энергии сигнала в небольшом числе коэффициентов. В этом смысле недостаток преобразования Фурье или косинусного преобразования состоит в том, что базисные функции равномерно разнесены по шкале частот. Это означает, что всем частотам уделяется одинаковое внимание. Из физических соображений следует, что следовало бы больше внимания уделить низкочастотным составляющим и меньше - высокочастотным, т.е. разрешающая способность системы функций должна быть неравномерной по частоте. Задачу построения такой системы функций частично удается решить с использованием теории вейвлетной (wavelet) фильтрации.
При вейвлетной фильтрации сигнал раскладывается с помощью двух фильтров на низкочастотную и высокочастотную составляющие. Высокочастотная составляющая, содержащая небольшую часть энергии, кодируется малым числом бит, а низкочастотная - раскладывается на две составляющие и т.д. При надлежащем выборе фильтров и распределении битовых затрат между компонентами сигнала такой подход позволяет обеспечить приблизительно вдвое больший коэффициент сжатия по сравнению со стандартом JPEG при одинаковом качестве восстановленных изображений.
Итак, основная идея вейвлетного преобразования сигнала состоит в иерархическом разложении входного сигнала на последовательности так называемых базовых (reference) сигналов с последовательно уменьшающимся разрешением и связанных с ними сигналов деталей (detail signals). На каждом уровне разложения базовый сигнал и сигнал деталей содержат информацию, необходимую для восстановления базового сигнала на следующем уровне с более высоким разрешением.
Одномерное дискретное вейвлетное разложение может быть описано в терминах банка фильтров. Входной сигнал x(n) фильтруется низкочастотным фильтром h0 (n) и высокочастотным фильтром h1(n). Далее производится децимация (прореживание)
отсчетов выходных сигналов фильтров с коэффициентом 2. Децимированный результат фильтрации низкочастотным фильтром r1(n) представляет собой базовый сигнал, а децимированный результат фильтрации высокочастотным фильтром d1(n) - это сигнал
деталей для одного уровня разложения. Очевидно, такая схема преобразует N отсчетов входного сигнала в две последовательности по N/2 отсчетов. В теории банков фильтров и в теории вейвлетной фильтрации найдены такие пары фильтров h0(n) и h1(n), для которых существует пара обратных фильтров, обеспечивающих точное восстановление исходного сигнала.
На рис. 5 показана схема одного уровня вейвлетного разложения. Для восстановления сигнала из базового сигнала и сигнала деталей производится интерполяция этих сигналов с коэффициентом 2, т.е. последовательность отсчетов базового сигнала и сигнала деталей расширяется путем вставки в нее через один отсчет нулевых отсчетов. Затем выполняется фильтрация интерполированных последовательностей соответственно низкочастотным и высокочастотным фильтрами g0(n) и g1(n). Сумма результатов фильтрации представляет собой выходной сигнал y(n). Система вейвлетной фильтрации (в отсутствие квантования) обладает свойством точного восстановления, т.е. выходной сигнал y(n) = Ax(n - а), где A-это коэффициент усиления, а- задержка.

Рисунок 5 – Один уровень вейвлетного разложения
В случае многоуровневой декомпозиции базовый сигнал r1(n) служит входом банка фильтров, аналогичного банку фильтров первой ступени. Процесс, который повторяется итеративно, показан на рис.6. После L уровней разложения он порождает сигнал rL(n) с разрешением, уменьшенным с коэффициентом 2L по отношению к исходному сигналу и сигналы деталей dL(n), dL1(n),...d1(n). Каждый сигнал деталей di(n) содержит информацию, которой совместно с базовым сигналом ri(n) достаточно для восстановления ri-1(n), который является базовым сигналом со следующей степенью разрешения.

Рисунок 6 – Многоуровневое вейвлетное разложение
Особенностью вейвлетного банка фильтров является то, что с ним связаны, так называемые, шкалирующая функция и вейвлет. Шкалирующие функции φA(x) и φS(x)удовлетворяют следующим уравнениям

и
 .
.
Вейвлеты ψА(х) и ψS(х) выражаются через шкалирующие функции
 ,
,
и
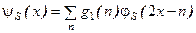 .
.
Необходимость рассмотрения вейвлетов и шкалирующих функций вытекает из следующих ограничений на банки фильтров, вводимых в теории вейвлетов:
- идеальное (точное) восстановление,
- существование обратных фильтров g0(n) и g1(n) с конечным импульсным откликом,
- требование регулярности, означающее, что итерированный сигнал на выходе низкочастотного фильтра сходится к непрерывной функции.

Рисунок 7 – Вейвлетное разложение изображения
При использовании вейвлетного преобразования для разложения сигнала изображения вначале выполняется разложение по строкам, а затем по столбцам. Результатом разложения являются 4 матрицы: HH0, HL0, LH0, LL0, соответствующие фильтрации фильтром h1(n) по строкам и h1(n) по столбцам, фильтром h1(n) по строкам и h0(n) по столбцам, фильтром ho(n) по строкам и h1(n) по столбцам, фильтром h0(n) построкам и столбцам. Далее низкочастотная матрица LL0 подвергается вейвлетному разложению. Его результатом являются матрицы: HH1, HL1, LH1, LL1. Такое разложение повторяется r раз, как показано на рис.7. Результатом разложения является набор из 3r+1 матриц уменьшающейся размерности. Каждая матрица подвергается скалярному или векторному квантованию и последующему кодированию. Выбор числа уровней квантования или шага квантования производится исходя из требуемого сжатия и соответствующего распределения битов между матрицами.
Высокочастотные матрицы (матрицы деталей), как правило, после квантования содержат большое число нулевых элементов. Одним из широко используемых методов кодирования матриц деталей является кодирование длин серий нулей и следующих за ними значений кодом Хаффмана. Низкочастотные матрицы непосредственно кодируются кодом Хаффмана.