Лекция 4. Тепловые процессы в идеальном газе.
Будем рассматривать квазистатические тепловые процессы в идеальном газе, в которых термодинамические параметры 
одинаковы во всем объеме газа, но при этом они изменятся со временем. Можно считать, что в таких процессах во все моменты времени выполняется уравнение Клапейрона – Менделеева
.
1. Изохорический процесс (
).
В таком процессе 
,
, 
, 
.
2. Изобарический процесс (
).
Здесь 
, 
, 
, 
.
3. Изотермический процесс (
).
В этом процессе 
,
,
.
4. Адиабатический процесс (
).
Тепловой процесс с телом, в котором оно не обменивается теплом с другими телами, назы-вается адиабатическим. Из первого начала термодинамики следует, что в таком процессе 
. Для идеального газа 
, поэтому при адиабатическом расширении идеаль-ный газ охлаждается, а при адиабатическом сжатии – нагревается.
Для одного моля идеального газа
, или 
.
Производя интегрирование, получаем
, 
.
Возводя последнее выражение в степень 
и используя уравнение Майера, приходим к уравнению
.
Это так называемое уравнение Пуассона для адиабатического процесса в идеальном газе. С помощью уравнения Клапейрона - Менделеева его можно представить в следующих формах
, или 
.
Из уравнения Пуассона видно, что если из одного и того же начального состояния с идеальным газом производится либо изотермический процесс (изотерма на рис. 4), либо адиабатический процесс (адиабата), то адиабата лежит ниже изотермы.
Типичным примером адиабатического процесса в идеальном газе является звуковая волна, которую мы рассмотрели в курсе механики. В этом случае успевает установиться локальное равновесие, но перенос тепла между областями с разным давление произойти не успевает.
Все рассмотренные выше процессы происходят при постоянной теплоемкости. Можно ввести еще один тип процессов в идеальном газе.
5. Политропический процесс (
).
Аналогично случаю адиабатического процесса с помощью первого начала термодинамики для такого процесса можно получить уравнение политропы
, где 
- показатель политропы.
Для адиабатического процесса 
, 
, для изотермического - 
, 
, для изохорического - 
, 
, для изобарического - 
, 
.
Лекция 5. Распределение молекул идеального газа по координатам и скоростям.
1. Идеальный газ во внешнем поле.
Рассмотрим малый элемент объема идеального газа, заключенный между двумя площадками 
, перпенди-кулярными потенциальной внешней силе 
и отстоя-щими друг от друга на расстоянии 
(рис. 1). Ось 
направлена противоположно силе . Давления газа на верхней и нижней площадках равны соответственно 
и 
. Тогда условие равновесия выделенного объема можно представить в виде
, или 
,
где 
- потенциальная энергия молекулы газа. Будем считать, что температура газа 
постоянна во всем объеме. Из уравнения Клапейрона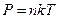 
(локальное равновесие) получим
, 
.
Интегрируя это уравнение, получаем формулу Больцмана для распределения молекул идеального газа по координатам во внешнем потенциальном поле
.
Здесь 
- концентрация молекул газа в точке 
, в которой 
. Аналогично для давления
. В поле тяжести 
.
Последнее выражение носит название барометрической формулы. На ней основано устрой-ство альтиметра – прибора для определения высоты над поверхностью Земли.
2. Распределение молекул по скоростям.
Мы уже ввели понятие средней квадратичной скорости молекул 
. Но молекулы в газе движутся с разными скоростями и важно определить какая часть молекул имеет скорости в определенном интервале значений. Рассмотрим интервал значений проекции скорости 
между и 
. Число молекул в единице объема с такими значениями можно представить в виде
. (1)
Функция 
в этом выражении называется функцией распределения по проекции скорости .
Вероятностный смысл можно пояснить, если переписать выражение (1) по другому
.
Таким образом, вероятность того, что проекция скорости молекул лежит в интервале от до равна 
.
Понятие вероятности вводится при изучении случайных событий различной природы. Дадим простейшее определение вероятности события:
,
где 
- число опытов, приводящих к реализации данного события, 
- общее число опытов. Например, при многократном бросании монеты вероятности выпадения ее каждой стороны 
, 
. Сумма этих вероятностей 
.Событие, вероятность которого равна единице называется достоверным (оно выполняется всегда). Одна из сторон монеты обязательно выпадет. Этот простой пример отражает одну из основных теорем теории вероятностей.
Теорема сложения вероятностей.
Если 
- вероятности исключающих друг друга событий, то вероятность того, что осуществится какое-нибудь одно из них
.
Имеет место также теорема для вероятности независимых событий. Например, бросание монеты и следующая за этим попытка сдать экзамен.
Теорема умножения вероятностей.
Вероятность совмещения нескольких независимых событий равна произведению вероят-ностей каждого из них в отдельности
.
Вычисление средних значений.
Пусть 
- число наблюдений значения 
случайной величины 
, - полное число наблюдений. Тогда среднее значение величины можно вычислить по формуле
,
где 
- вероятность того, что величина примет значение . Тогда среднее значение проекции скорости молекулы можно представить в виде
.
Получим явный вид функции распределения . Попадания скоростей молекул в интервалы 
, 
, 
являются независимыми событиями. Значит вероятность попадания вектора скорости 
сразу в три эти интервала равна
.
Из хаотичности теплового движения молекул вытекает свойство четности функции распределения
, или 
.
Удобно ввести переменные 
, 
, 
. Тогда для функции распределения по скоростям справедливы соотношения
. (2)
Рассмотрим такие изменения 
, которые удовлетворяют соотношениям 
, 
. Тогда из (2) получим
(введем такое обозначение).
Решая это дифференциальное уравнение, находим
. (3)
Для функции распределения выполняется условие нормировки
,
означающее, что попадание в интервал от 
до 
является достоверным событием. Подставляя в это условие выражение (3), находим константу 
.
Константу 
можно найти с помощью равенства
.
Проводя интегрирование, находим 
. Подставляя и в выражение (3), получаем распределение Максвелла по проекции скорости молекул на ось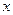 
.
С помощью соотношения (2) легко получить функцию распределения по всем проекциям скорости молекул
.
Если газ находится во внешнем потенциальном поле то можно рассматривать более общее распределение по полной энергии молекул 
,
называемое распределением Максвелла – Больцмана.
Рассмотрим распределение молекул по модулю скорости. Вероятность найти молекулу в пространстве скоростей в элементе объема 
в окрестности скорости
.
Для нахождения вероятности того, что молекула имеет модуль скорости в интервале от 
до 
мы должны в качестве взять в качестве элементарного объема шаровой слой радиуса и толщиной 
. В этом случае 
и функция распределения по модулю скорости принимает вид
.
Эта функция имеет максимум при 
. Величина 
называется наивероятнейшей скоростью молекул газа (рис. 2). При этом 
.
Лекция 6. Экспериментальные подтверждения молекулярно-кинетической теории. Броуновское движение.
Опыт Штерна.
В этом опыте (1920 г.) экспериментально проверялось распределение Максвелла для молекул идеального газа. Установка представляла собой два жестко соединенных коаксиальных цилиндра на оси которых располагалась платиновая нить, покрытая серебром (рис. 1). Нить нагре-валась до температуры 12000С проходящим через нее электрическим током. Газ из молекул серебра из малого цилиндра вытекал через узкое отверстие. Молекулы серебра оседали на внутренней поверхности большого цилиндра и по их числу можно было определить их распределение по скоростям. Это можно сделать следую-щим образом. При неподвижных цилиндрах молекулы попадают в точку 
. В случае вращения с угловой скоростью 
молекула, движущаяся со скоростью , попадает в точку 
, отстоящую от на расстоянии
, откуда 
, 
.
Число молекул со скоростями от до , испускаемых нитью в 1 секунду
.
Проведенные Штерном измерения толщины слоя осевшего серебра с большой точностью соответствовали этому выражению. Значения скоростей изменялись примерно от 540 м/сек до 640 м/сек, а 
580 м/сек.
Распределение Максвелла и атмосферы планет.
При столкновении молекул в атмосфере планеты они могут приобретать скорости, превыша-ющие вторую космическую скорость 
. Такие молекулы покидают атмосферу планеты (убегающие молекулы). Такой процесс называется рассеянием атмосферы. Число молекул, покидающих атмосферу в единицу времени можно определить с помощью выражения
,
где 
- распределение Максвелла по модулю скорости, - площадь поверхности планеты, 
- концентрация молекул у ее поверхности. Множитель 
появляется после усреднения по всем углам падения молекул по отношению к поверхности , 
-средняя скорость убегающих молекул
.
Пренебрегая кривизной поверхности планеты, можно оценить полное число молекул в атмосфере по формуле Больцмана
.
С помощью приведенных соотношений можно получить уравнение
, 
- время рассеяния атмосферы, 
.
Для Земли 
км/сек, 
9.8 м/сек2 . Отсюда при 
3000К для атомарного водорода 
27 лет, а для молекулярного водорода 2ּ1012 лет.
Броуновское движение.
Одним из убедительных доказательств молекулярно-кинетической теории является так называемое броуновское движение, открытое в 1827 г. английским ботаником Броуном.
Он обнаружил, что при рассмотрении под микроскопом частицы, взвешенные в жидкости, находятся в непрерывном беспорядочном движении. Оно возникает вследствие ударов со стороны движущихся молекул жидкости. На основе такого представления Эйнштейном и Смолуховским была построена теория броуновского движения (1906 г.). Ее основные положения состоят в следующем. Движение крупной (по сравнению с размером молекул) частицы массы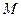 
в жидкости можно описать в проекции на ось 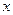с помощью уравнения
, (1)
где первое слагаемое в правой части представляет собой силу вязкого трения по формуле Стокса, а 
есть сила случайных толчков со стороны молекул жидкости. Назовем подвижностью частицы величину 
. После несложных преобразований можно привести уравнение (1) к следующему виду
. (2)
Усредним уравнение (2) по всем броуновским частицам. В силу хаотичности движения молекул 
. Так как броуновские частицы находятся в тепловом равновесии с моле-кулами жидкости, то 
. При таких предположениях после усреднения получим
.
Решение этого уравнения имеет вид 
и называется формулой Эйнштейна. Она была экспериментально подтверждена в опытах Перрена в 1908 г.
Лекция 7. Явления переноса и столкновения молекул в газе.
Переход от неравновесных состояний к равновесным происходит благодаря явлениям переноса. При этом происходит выравнивание значений термодинамических параметров. В зависимости от вида переносимых физических величин можно выделить три явления переноса.
1. Диффузия.
При диффузии происходит перенос массы и выравнивание плотности. Пусть плотность газа 
меняется вдоль оси 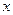. Опытным путем был получен закон диффузии
, (1)
где 
- масса вещества, переносимая через площадку 
, перпендикулярную оси 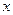, за время 
. Коэффициент называется коэффициентом диффузии, 
1 м2/сек. Знак “-” означает, что перенос массы происходит в направлении уменьшения плотности. Величина 
является проекцией градиента плотности на ось 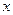. В дальнейшем мы будем называть ее просто градиентом плотности.
2. Теплопроводность.
В этом процессе происходит перенос тепла и выравнивание температуры. При изменении температуры вдоль оси 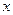закон теплопроводности имеет вид
,
где 
- количество тепла, переносимого через площадку , перпендикулярную оси 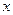, за время . Коэффициент 
называется коэффициентом теплопроводности, 
1 Дж/мּсекּград, 
- градиент температуры.
3. Внутреннее трение.
Происходит перенос импульса между слоями газа (жидкости), движущимися друг относи-тельно друга. При этом между слоями возникает сила вязкого трения
,
где ось 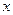перпендикулярна скорости течения газа 
, - площадка слоя газа с коорди-натой ,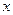 
- коэффициент вязкости, 
1 кг/мּсек = 1 г/смּсек = 1 Пуаз, 
- градиент скорости.
Процессы переноса в газе происходят в результате столкновений молекул. Рассмотрим основные величины, используемые для описания столкновений.
Средняя длина свободного пробега молекул 
– среднее расстояние между двумя последовательными столкновениями.
Эффективное сечение столкновений.
Если молекула с радиусом 
налетает на другую такую же молекулу, то они столкнутся, если расстояние между их центрами не превышает 
(рис. 1). Площадь заштрихованной окружности 
называется эффективным сечением столкновений.
Если центр налетающей молекулы попадает в заштрихованную площадку 
(прицельная площадь) , то молекулы сталкиваются. Эффективное сечение столкновений имеет также вероятностный смысл. Можно показать, что величина численно равна вероятности столкновения молекулы в единице объема.
Число столкновений молекулы за 1секунду
. (2)
Это выражение можно получить, рассмотрев цилиндрический объем с площадью основания и высотой (рис. 2). Здесь - средняя скорость молекул. Очевидно, молекула в левом основании цилиндра столкнется со всеми молекулами внутри выделенного объема. На самом деле, после каждого столкновения направление движения выделенной молекулы изменяется и цилиндр становится лома-ным. Однако, формула (2) при этом не изменяется.
С помощью (2) можно получить выражение для длины свободного пробега . Очевидно,
.
При получении (1) мы считали молекулы внутри выделенного цилиндра неподвижными. Можно уточнить выражение для , если учесть относительное движение молекул. Легко показать, что средняя скорость относительного движения 
. Отсюда
. (3)
Приведем характерные значения величин и . Для воздуха при 00С и = 1 атм 
см-3 , 
см2, 
см.
Как было отмечено выше, явления переноса в газе происходят в результате столкновений молекул. Поэтому коэффициенты переноса должны зависеть от длины свободного пробега и средней скорости молекул. Рассмотрим эту зависимость для процесса диффузии.
Как и в законе диффузии (1) будем считать, что плотность газа меняется вдоль оси .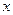
Рассмотрим малую площадку , перпендикулярную этой оси . Если бы все молекулы двигались слева направо со скоростью 
, то через за время проходила бы масса газа 
. Пусть 
- плотности газа соответственно слева и справа от площадки на расстоянии . Тогда в силу того, что в этих промежутках нет столкновений, слева направо через за время проходит масса
.
Множитель 
появляется из-за того, что в среднем 
молекул движется вдоль ос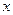и и 
от этого количества – слева направо.
Аналогично справа налево проходит масса
.
Тогда полная масса газа, проходящая через площадку за время
. (4)
Пусть на площадке значение плотности равно 
. Тогда в виду малости можно записать
, 
, 
.
Подставляя последнее выражение в (4), получим
, 
.
Аналогичным образом можно получить
, 
.
В проведенном анализе мы считали молекулы твердыми шариками радиуса . В такой модели из выражения (3) следует длина свободного пробега не зависит от температуры. Тогда можно считать, что 
или 
. Средняя скорость молекул идеального газа 
. Отсюда 
при и 
при 
. Из выражений дляи следует, что эти коэффициенты переноса не зависят от 
при и пропор-циональны 
при .
Лекция 8. Нестационарные процессы переноса. Перенос в разреженных газах.
Процессы переноса называются стационарными, если градиент соответствующей физичес-кой величины не зависит от времени. Такой процесс возможен только при наличии соответ-ствущих источников. Например, в процессе стационарной теплопроводности всегда при-сутствует источник тепла и некоторые тела, поглощающие тепло. При этом градиент температуры не меняется со временем в каждой точке. Удобно для описания процессов переноса использовать понятие потока соответствующей переносимой величины. Например, поток тепла 
равен количеству тепла, переносимому в единицу времени через единицу площади перпендикулярно к направлению градиента температуры
.
Тогда уравнение теплопроводности можно представить в виде
. (1)
Отсюда следует, что при стационарной теплопроводности поток тепла в любой плоскости, перпендикулярной к направлению градиента температуры не изменяется со временем.
В нестационарных процессах переноса градиенты физических величин изменяются со временем. При этом, если нет внешних источников, происходит выравнивание этих величин по всему объему. В этом случае важно выяснить, как зависит время установления равнове-сия от параметров физической системы.
Рассмотрим конкретный процесс нестационарной теплопроводности. Два сосуда с газом с объемами 
, 
и начальными температурами 
, 
соединены трубкой длины 
с площадью поперечного сечения (рис. 1). Пусть 
. Будем считать, что вдоль трубки температура изменяется линейно
, где 
.
За время из одного сосуда в другой перейдет количество тепла
.
При этом в сосуде 1 температура уменьшится на 
, а в сосуде 2 – увеличится на 
. Пусть плотность газа равна , а его удельная теплоемкость при постоянном объеме равна 
. Тогда изменения температуры газа в сосудах можно представить в виде
.
Тогда изменение разности температур 
за время
.
Таким образом, мы пришли к дифференциальному уравнению для :
, где 
- постоянная времени теплопроводности , 
-
приведенный объем. Решение этого уравнения имеет вид
, 
- начальная разность температур газа в сосудах.
Следовательно, постоянная времени теплопроводности 
равна характерному времени выравнивания температуры. В выражении для удобно выделить сомножитель, зависящий только от свойств газа
, называемый коэффициентом температуропроводности.
Аналогичным образом можно рассмотреть процесс нестационарной диффузии. В этом случае процесс выравнивания плотности определяется постоянной времени диффузии
.
Общее уравнение нестационарной теплопроводности.
Рассмотрим изменение количества тепла в малом объеме, заключенном между двумя площадками 
перпендикулярными оси 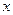и отстоящими слева и справа от точки 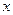на расстоянии 
(рис. 2). Будем также как и выше считать, что поток тепла имеет место только вдоль оси 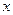. Тогда изменение количества тепла в объеме 
за время 
равно
.
С помощью разложения 
в ряд Тейлора в окрестности точки 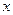, а также используя уравнение (1), получим
.
С другой стороны можно вычислить 
через теплоемкость и изменение температуры
Поделив два последних уравнения на 
и перейдя к пределу при 
, получим уравнение теплопроводности
.
Явления переноса в разреженных газах.
Разреженный газ (вакуум) – длина свободного пробега молекул сравнима или больше, чем характерный размер сосуда , в котором находится газ, то есть 
. В этом случае роль длины свободного начинает выполнять среднее расстояние между ударами о стенки и при вычислении коэффициентов переноса можно положить 
.
Теплопроводность в разреженном газе.
Для идеального газа в обычных условиях (лекция 7) . В разреженном газе , поэтому плотность не сокращается за счет зависимости и возникает линейная зависи-мость от давления газа
(
- масса молекулы газа), то есть 
.
Такая зависимость реализуется в сосудах с двойными стенками, между которыми находится разреженный газ (сосуд Дьюара, термос). Чем меньше давление разреженного газа тем меньше теплопроводность стенок такого сосуда.
Вытекание разреженного газа через малое отверстие (эффузия).
Отверстие считаем малым, если его диаметр 
. Тогда скорость вытекания молекул газа
. (2)
Если при этом в сосуде находится смесь газов, то быстрее вытекает более легкая компо-нента. Это явление используется для разделения изотопов.
Эффект Кнудсена.
Если два сосуда с газом соединены тонкой трубкой с диаметром 
, то при равновесии
. Тогда из (2) следует связь между давлениями и температурами 
.
Лекция 9. Тепловые машины. Теоремы Карно.
Из опыта известно, что работу можно произвести только с помощью тел, не находящихся в тепловом равновесии. Но если просто соединить два тела с разными температурами, то система через некоторое время придет к состоянию равновесия и мы в дальнейшем не получим никакой работы. Чтобы вернуть систему в первоначальное состояние, мы должны произвести некоторые изменения в данной системе и в окружающих телах. В связи с этим возникает важное понятие обратимости и необратимости тепловых процессов.
Обратимые процессы.
Процесс в термодинамической системе называется обратимым, если возможно осуществить его в обратном порядке, проходя через все его промежуточные состояния без изменения состояния внешних тел.
Так как каждое состояние в квазистатическом процессе является равновесным, то такой процесс можно считать обратимым.
Необратимые процессы.
Если для данного процесса невозможен обратный процесс без изменения во внешних телах, то он называется необратимым.
Все процессы, сопровождающиеся теплопередачей от нагретого тела к менее нагретому являются необратимыми. Существует много других необратимых процессов, которые мы рассмотрим в дальнейшем.
Тепловая машина.
Любая тепловая машина состоит из трех основных элементов (рис. 1): нагревателя, рабочего тела и охладителя. Ее работа имеет циклический характер. В каждом цикле рабочее тело получает от нагревателя количество тепла 
и отдает охладителю теплоту 
. За каждый цикл совершается работа 
. Здесь 
, 
. Эффективность работы тепловой машины характеризуется коэффициентом полезного действия (к.п.д.)
Из сказанного выше можно заключить, что с помощью тепловой машины можно получить максимально возможную работу, если тепловые процессы в ней происходят обратимым образом. На практике это невозможно, так как всегда имеет место контакт тел с разными температурами. Для вычисления максимально возможной работы следует рассмотреть идеальную тепловую машину, в которой все процессы обратимы.
Идеальная тепловая машина. Цикл Карно.
В идеальной тепловой машине рабочим телом являет-ся идеальный газ. С рабочим телом в каждом цикле про-изводится обратимый круговой процесс, назы-ваемый циклом Карно (рис. 2). Он состоит из двух изотерм (
и
) и двух адиабат (
и
). На участке рабочее тело получает тепло от нагрева-теля, а на участке – отдает тепло охладителю.
Для вычисления к.п.д. достаточно вычислить работы 
и 
на изотермах. Работа газа на изотерме
.
Из уравнения Пуассона для адиабаты следует, что 
. Аналогично для получим
, где 
.
Учитывая, что на изотермах 
и 
отсюда можно получить формулу Карно для к.п.д. идеальной тепловой машины
.
Имеют место следующие фундаментальные теоремы Карно.
Теорема 1.
К.п.д. тепловой машины, работающей при данных значениях температур нагревателя и охладителя, не может быть больше, чем к.п.д. машины, работающей по обратимому циклу Карно при тех же температурах нагревателя и охладителя.
Теорема 2.
К.п.д. идеальной тепловой машины не зависит от рабочего тела, а определяется лишь температурами нагревателя и охладителя.
Лекция 10. Второе начало термодинамики. Энтропия.
Теоремы Карно явились основой для формулировки второго начала термодинамики (или второго закона термодинамики). Этот фундаментальный закон природы позволяет количест-венно описать направленность процессов в термодинамических системах. Из него также следует ряд общих термодинамических соотношений, справедливых для любого состояния вещества. Существует несколько различных формулировок этого закона.
Первая формулировка второго начала термодинамики (принцип Томсона).
Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара.
Если бы такой процесс был возможен, то это означало бы возможность вечного двигателя второго рода, который мог бы непрерывно совершать работу, поглощая, например, теплоту от нагретой Солнцем океанской воды. При этом, в отличие от широко известного вечного двигателя первого рода, закон сохранения энергии не нарушался бы.
Можно записать выражение для к.п.д. цикла Карно в виде
, или 
.
Последнее соотношение представляет собой частный случай равенства Клаузиуса для произвольного обратимого кругового процесса
.
По первой теореме Карно для тепловой машины с необратимым круговым процессом
, то есть 
.
В общем случае необратимого кругового процесса имеет место неравенство Клаузиуса
.
Эти соотношения в дальнейшем привели к понятию одной из важнейших физических величин – энтропии.
Для бесконечно малого обратимого изменения состояния термодинамической системы изменение ее энтропии определяется как
.
При этом является полным дифференциалом. Это следует из равенства Клаузиуса, так как при возвращении в исходное состояние энтропия остается неизменной независимо от конкретного вида кругового процесса. Отсюда, в частности, вытекает еще одна формули-ровка второго начала термодинамики.
Вторая формулировка второго начала термодинамики.
Энтропия термодинамической системы, находящейся в равновесном состоянии, является однозначной функцией этого состояния.
Рассмотрим изменение энтропии замкнутой термодинамической системы. Очевидно, в обра-тимых процессах 
, так как в этом случае суммарное малое изменение .
Для того, чтобы определить, как изменяется энтропия в необратимых процессах, рассмотрим круговой процесс, состоящий из необратимого процесса 1 – 2 и обратимого процесса 2 – 1 (рис. 1). При этом на этапе 1 – 2 система является замкнутой, а на этапе 2 – 1 – незамкнутой. Тогда для полного кругового необратимого процесса выпол-няется неравенство Клаузиуса
.
Так процесс 2 – 1 является обратимым, то отсюда получим
.
На этапе 1 – 2 система является замкнутой, поэтому здесь . Таким образом измене-ние энтропии замкнутой системы в необратимом процессе
.
Отсюда вытекает третья формулировка второго начала.
Третья формулировка второго начала термодинамики.
Энтропия замкнутой термодинамической системы не убывает при любых происходящих в ней процессах. В необратимых процессах она возрастает, а в обратимых – остается неизмен-ной.
Энтропия одного моля идеального газа.
Первое начало термодинамики для одного моля идеального газа в бесконечно малом обратимом процессе можно записать в виде
.
Отсюда получаем
, 
.
В силу того, что энтропия является аддитивной величиной (пропорциональна массе) для молей идеального газа
. (1)
В силу дифференциального характера определения энтропии, она так же как и потенциаль-ная энергия в механике, определена с точностью до произвольной константы.
Вычислим изменение энтропии в конкретных необратимых процессах с идеальным газом.
1. Расширение газа в вакуум.
Рассмотрим идеальный газ, находящийся в одной части сосуда с жесткими теплоизоли-рованными стенками (рис. 2). В другой части сосуда, отделенной от первой перегородкой, имеет место вакуум. Будем считать, что перегородка убирается таким образом, чтобы газ при этом не мог совершить работу. В том случае 
, 
(теплоизоляция) и из первого начала термодинамики следует, что 
. Для идеального газа при этом 
. Тогда изменение энтропии одного моля идеального газа в таком процессе
,