Дифференциальная форма теоремы Гаусса

Дифференциальная (или локальная) форма теоремы Гаусса расширяет ее возможности как инструмента исследования и расчета, Форму (3-2) называют интегральной теоремой Гаусса. В дифференциальной форме теоремы устанавливается связь между объемной плотностью заряда и изменениями напряженности поля в окрестности данной точки пространства.

Для этого представим сначала заряд q в объеме V, охватываемом замкнутой поверхностью S, как q = ρ_ср V, где ρ_ср − среднее по объему V значение объемной плотности заряда. Затем подставим это выражение в уравнение (3-2) и разделим обе части его на V. В результате получим

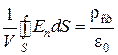. (3-10)

Теперь устремим объем V к нулю, стягивая его к интересующей нас точке поля. Очевидно, при этом r_ср будет стремиться к значению r в данной точке поля, а значит, отношение в левой части уравнения
(3-10) будет стремиться к ρ_ср /ε₀ .

Величину, являющуюся пределом правой части этого равенства при V ® 0, называют дивергенцией поля 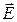и обозначают div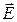. Таким образом, по определению:

. (3-11)

Аналогично определяется дивергенция любого другого векторного поля. Из определения (3-11) следует, что дивергенция является скалярной функцией координат. Чтобы получить выражение для дивергенции поля 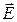, надо согласно (3-11) взять бесконечно малый объем V, определять поток вектора 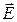через замкнутую поверхность, охватывающую этот объем, и найти отношение этого потока к объему. Полученное выражение для дивергенции будет зависеть от выбора системы координат (в разных системах координат оно оказывается разным). Например, в декартовой системе координат:

.

Таким образом, при V ® 0 в выражении (3-10) его правая часть стремится к r_ср /ε₀ , а левая – к div. Следовательно, дивергенция поля 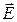связана с плотностью заряда в той же точке уравнением

. (3-12)

Это уравнение и выражает теорему Гаусса в дифференциальной форме. В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция напряженности поля в данной точке зависит только от плотности электрического заряда ρ в той же точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле отличается друг от друга. Это же относится, вообще говоря, и к пространственным производным ¶E_x /¶x, ¶E_y /¶y, ¶E_z /¶z. Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет дивергенцию , оказывается во всех точках поля (вне самого заряда) равной нулю.

В тех точках поля, где дивергенция 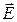положительна, мы имеем источники поля (положительные заряды), а в тех точках, где она отрицательна, − стоки (отрицательные заряды). Линии вектора 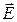выходят из источников поля, а в местах стоков они заканчиваются.