Пример решения СЛАУ итерационными методами.
Дана система уравнений

Выполним проверку выполнения достаточного условия сходимости.
Проверяем условие диагонального преобладания.
первое уравнение: 4>1+1=2 – выполняется;
второе уравнение: 2<1+5=6 – не выполняется;
третье уравнение: |–1|<1+6=7 – не выполняется.
Таким образом, условие диагонального преобладания для исходной системы уравнений не выполняется и поэтому не может быть гарантирована сходимость итерационных методов к решению. Для данной системы можно добиться выполнения этого условия перестановкой второго и третьего уравнений:

Проверяем условие диагонального преобладания для преобразованной системы:
первое уравнение: 4>1+1=2 – выполняется;
второе уравнение: 6>1+|–1|=2 – выполняется;
третье уравнение: 5>1+2=3 – выполняется.
Решение СЛАУ методом простой итерации.
Схема пересчета в данном случае имеет вид:
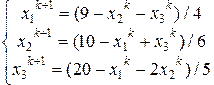
Начальное приближение: 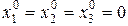 .
.
Для определения точности приближения воспользуемся нормой вектора
 – максимум модуля для элементов вектора.
– максимум модуля для элементов вектора.
Первый шаг итерации ( ):
):
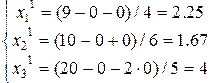
 .
.
Второй шаг итерации ( ):
):

 .
.
Третий шаг итерации ( ):
):

 .
.
После трех итерационных шагов получаем приближенное решение СЛАУ:  .
.
Решение СЛАУ методом Зейделя.
Схема пересчета в данном случае имеет вид:

Начальное приближение: 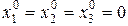 .
.
Первый шаг итерации ( ):
):

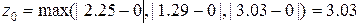 .
.
Второй шаг итерации ( ):
):


Третий шаг итерации ( ):
):

 .
.
После трех итерационных шагов получаем приближенное решение СЛАУ:  .
.
При том, что точное решение данной СЛАУ:  , – отметим большую точность решения. полученного методом Зейделя по сравнению с методом простой итерации за одинаковое количество итерационных шагов.
, – отметим большую точность решения. полученного методом Зейделя по сравнению с методом простой итерации за одинаковое количество итерационных шагов.