Выигрыш в отношении сигнал-шум про оптимальной линейной фильтрации.

 

Введем понятие выигрыш в отношении сигнал-шум.

Числитель – отношение сигнал-шум по мощности на выходе оптимального фильтра.

Р_{с вых} – средняя мощность сигнала на выходе,

Р_{ш вых} – средняя мощность шума на выходе.

Знаменатель – отношение сигнал-шум по мощности на входе оптимального фильтра.

Р_{с вх} – средняя мощность сигнала на входе,

Р_{ш вх} – средняя мощность шума на входе.

Для сигнала а постоянной огибающей средняя мощность

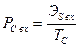
Формально мощность белого шума равна бесконечности, но в фильтр проходит только мощность в пределах полосы пропускания.

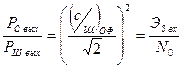
, где Т_с [Δf_{s вх}] – база входного сигнала (величина безразмерная).

Выигрыш в отношении сигнал-шум при оптимальной фильтрации численно равен базе входного сигнала, с которым согласован фильтр.

Как известно все сигналы делятся на две группы, в зависимости от величины базы:

- простые Т_с [Δf_{s вх}]≈1,

- сложные Т_с [Δf_{s вх}]>>1.

Таким образом выигрыш в отношении сигнал-шум получается только для сложных сигналов.

Для простых сигналов выигрыша нет, но нет и проигрыша, который получается при не оптимальном фильтре.

Пример: Т_с [Δf_{s вх}]=1000

тогда