В ВИДЕ СЕТЕЙ ПЕТРИ
Задачи исследования производственных комплексов могут быть решены путем воспроизведения и экспериментального изучения функционирования абстрактных систем. Процесс функционирования исследуемого объекта воспроизводит ЭВМ по специально разработанной моделирующей программе. В соответствии с этой программой ЭВМ осуществляет итоговое определение значений характеристик состояния абстрактной системы, выступающей в качестве систем формализованного управления исследуемого объекта.
В настоящее время сформировалась определенная методология имитационного моделирования, в соответствии с которой при построении моделей выполняются следующие этапы: конкретизация целей и задач исследования объекта; описание функционирования объекта и оценка возможностей формализации; построение формализованной модели; построение моделирующего алгоритма; разработка программы моделирования на ЭВМ; проверка работы (верификация) имитационной модели; обработка результатов моделирования и оценка пригодности имитационной модели.
На этапе определения целей и задач выявляются стороны процесса функционирования объекта, позволяющие найти границы исследования объекта. Установление таких границ весьма существенно влияет как на результаты формализованного описания этого объекта, так и на конечные результаты всего процесса создания имитационной модели.
Если исследование объекта сводится к воспроизведению процесса его функционирования, необходимо при формулировке задачи исследования указать, какие конкретные стороны рассматриваемого процесса должны быть воспроизведены.
Описание функционирования объекта отражает представление исследователя о сущности процессов в исследуемом объекте при их рассмотрении в границах, определяемых целями исследования. При описании сложных объектов всегда имеется опасность допустить ошибки при разработке алгоритмического и программного обеспечения. В этих случаях целесообразно использовать описание систем на функциональном и структурном уровнях, где значительно меньшие информационные потоки.
Представление модели системы на разных этапах разработки в виде функционально–структурной схемы дает определенные возможности для формализации описаний процессов. Используя методы формализованного представления процессов в дискретных системах (сети Петри и их расширения, ротационные сети и др.) с небольшим алфавитом представления взаимосвязей, удается избежать ошибок при дальнейшей разработке программного обеспечения. Возникает задача отыскания связей между функционально–структурным и параметрическим уровнями модели, обеспечивающими быстрый и наиболее простой перехода к разработке программ для ЭВМ.
Однако этот уровень формализации модели может быть еще не достаточным для отображения ее в алгоритмической форме; он представляет собой абстрактную систему, замещающую сам объект в целях его исследования.
Внутренняя структура системы может быть недостаточно детализирована, взаимосвязи между элементами могут иметь обобщенный характер. Однако на этом уровне появляется возможность сделать обоснованный выбор метода решения поставленных задач.
Формирование структуры системы во многом облегчается благодаря тому, что хорошо изучено несколько распространенных типов дискретных и непрерывных абстрактных систем (системы массового обслуживания, автоматные, агрегатные, потоко–уровневые и т.д.), которые могут быть применены для формализации весьма широкого класса объектов с учетом самых различных требований.
Процесс функционирования станочных систем носит случайный характер. Как правило, это приводит к необходимости многократного "проигрывания" имитационной модели с последующей статистической обработкой результатов моделирования.
Затраты времени на моделирование стохастических моделей значительно больше, чем на моделирование детерминированных.
Существующие функциональные модели объектов, на наш взгляд, не совсем соответствуют поставленным целям. Так, например, агрегативные модели разработаны прежде всего для описания информационных систем и относятся к классу объектов, которые принято изображать в виде преобразователей, функционирующих во времени t 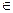 Г =[0,
Г =[0, 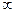 ] и способных воспринимать входные сигналы Х со значениями из некоторого множества Х, выдавать выходные сигналы У со значениями из множества Y и находиться в каждый момент времени в некотором состоянии z из множества Z. Класс кусочно–линейных агрегатов отличает специфика множеств Х, У, Z, допустимые формы входных и выходных сообщений (т.е. функции Х(t) и У(t), t
] и способных воспринимать входные сигналы Х со значениями из некоторого множества Х, выдавать выходные сигналы У со значениями из множества Y и находиться в каждый момент времени в некотором состоянии z из множества Z. Класс кусочно–линейных агрегатов отличает специфика множеств Х, У, Z, допустимые формы входных и выходных сообщений (т.е. функции Х(t) и У(t), t 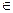 Т, траекторий Z(t), t
Т, траекторий Z(t), t 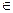 Т, а также способ преобразования входного сообщения в выходное.
Т, а также способ преобразования входного сообщения в выходное.
При использовании агрегативных моделей затруднительно отыскивать типовые модули, которые могли бы быть приняты за основу при переходе к алгоритмическому и программному уровням. Формально сеть Петри задается в виде тройки С = (Р, Т, Е), где Р – непустое конечное множество позиции сети; Т – непустое конечное множество переходов; Е = (Р х Т) 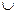 (Т х Р) –отношение инцидентности позиции и переходов.
(Т х Р) –отношение инцидентности позиции и переходов.

Традиционно сети Петри представляются двухдольными орграфами С = (Р 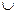 Т,Е). Множество вершин в таких орграфах состоит из непересекающихся подмножеств позиций Р = {p
Т,Е). Множество вершин в таких орграфах состоит из непересекающихся подмножеств позиций Р = {p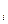 }, i =
}, i =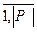 и переходов Т = {t
и переходов Т = {t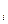 }, j =
}, j =  , а множество дуг Е разделяется на два подмножества: {(p
, а множество дуг Е разделяется на два подмножества: {(p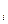 ,t
,t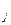 )}
)} 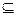 PxT и {(t
PxT и {(t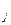 ,p
,p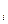 )}
)} 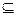 TxP. Дуги (p
TxP. Дуги (p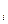 , tj) ориентированы от позиций к переходам, а дуги {(t
, tj) ориентированы от позиций к переходам, а дуги {(t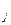 ,p
,p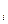 )}
)}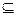 TxP. Дуги (p
TxP. Дуги (p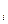 , t
, t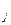 ) ориентированы от позиций к переходам, а дуги (p
) ориентированы от позиций к переходам, а дуги (p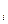 ,t
,t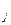 ) – от переходов к позициям.
) – от переходов к позициям.
Сети Петри являются удобным аппаратом моделирования параллельных процессов, протекающих в системе независимо друг от друга. На выполнение таких процессов не накладываются какие–либо условия синхронизации. Моменты начала и завершения параллельных процессов, интервалы их реализации не являются в системе взаимно обусловленными. Параллельным процессам соответствуют состояния сети Петри, в которых оказываются возбужденными сразу несколько переходов. Каждый из этих переходов может быть выполнен. Однако вопрос о том, какой переход будет выполняться, решается всякий раз случайным образом по правилам равновероятного выбора.
Действие такого механизма проявляется в свойстве недетерминированности сетей Петри. Ни два, ни более возбужденных в некотором состоянии сети переходов одновременно не выполняются. Всякий возбужденный переход готов для выполнения, но момент его фактического срабатывания не определен с той точностью, которая соответствует размещению событий на временной шкале. Иначе говоря, в сетях Петри не моделируется ход времени. Такой способ упорядочения обеспечивает выполнение сетей Петри.
При моделировании систем с помощью сетей Петри приходится следить за тем, чтобы все потенциальные возможности в сети последовательности событий соответствовали допустимым в рассматриваемых условиях процессам в системе, что особенно важно при наличии в модели большого числа параллельных процессов. В этом случае даже незначительные, а первый взгляд, неточности, допущенные при описанных реально наблюдаемых (или же возможных) взаимодействиях между компонентами процессов, могут привести к появлению тех последовательных событий, осуществление которых в модели будет не обосновано.
Формально временные сети задаются набором из пяти элементов TС= (Р, Т, Е, Мo, Z), где Р, Т, Е и имеют обычный для сети Петри смысл, а Z: Р  R+ – функция времени задержки меток в позиции сети. Правила перехода меток во временных сетях совпадают с аналогичными правилами для сетей Петри.
R+ – функция времени задержки меток в позиции сети. Правила перехода меток во временных сетях совпадают с аналогичными правилами для сетей Петри.
Временные сети являются существенной модификацией сетей Петри. Хотя и те и другие относятся к сетям событий и в основном предназначаются для моделирования и анализа системы с параллельными процессами, тем не менее они составляют два различных класса. Сеть Петри образует класс асинхронных сетей событий, в которых не учитывается продолжительность отдельных фаз процессов, а рассматривается только логическая (причинно–следственная) взаимосвязь событий. Временные сети – это сети событий синхронного типа. Изменение разметки производится в моменты срабатывания переходов.
Е–сети применяются в качестве имитационных моделей систем, структурованных в виде сетей события. Формально они определяются набором из восьми элементов:
Е = (Р, В, R), А, (I(A), O(A)), Z, V, Q,  , Mo)
, Mo)
Первый элемент набора означает: конечное непустое множество позиции сети Р = {pi}; множество периферийных (не внутренних) позиций В = {вк} = Р; множество решающих позиций R = {rm} = P.
Позиции Рi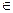 Р/R играют в Е–сети ту же самую роль, что и в сетях Петри. Их графические изображения также совпадают.
Р/R играют в Е–сети ту же самую роль, что и в сетях Петри. Их графические изображения также совпадают.
Периферийные позиции вk 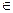 В Р используются для моделирования взаимосвязей системы с внешней средой. Решающие позиции не имеют прямых аналогов в сетях Петри. С их помощью в Е–сетях обеспечиваются разрешение конфликтов и синхронизация событий. В Е–сетях метки не накапливаются. Число меток в каждой позиции не может быть больше единицы (М:Р
В Р используются для моделирования взаимосвязей системы с внешней средой. Решающие позиции не имеют прямых аналогов в сетях Петри. С их помощью в Е–сетях обеспечиваются разрешение конфликтов и синхронизация событий. В Е–сетях метки не накапливаются. Число меток в каждой позиции не может быть больше единицы (М:Р {0,1} – функция разметки сети). Наличие метки в позиции на грифе Е–сети отмечается жирной точкой.
{0,1} – функция разметки сети). Наличие метки в позиции на грифе Е–сети отмечается жирной точкой.
Второй элемент набора соответствует конечному непустому множеству переходов А = {an}. На графических изображениях Е–сетей переходы, как и прежде, задаются барьерами.
Третий элемент (I(A), O(A) обозначает множество позиций, смежных с переходами по входу (I) и выходу (0). Пары (Pi,an) 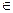 I (A)xA и (an,pi)
I (A)xA и (an,pi) 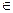 AxO(A) составлены из смежных позиций и переходов, соответствуют дугам сети.
AxO(A) составлены из смежных позиций и переходов, соответствуют дугам сети.
Четвертый элемент – это функция Z:A R+, с помощью которой в Е–сетях задаются значения времени выполнения переходов. Таким образом имитируются временные задержки, связанные с реализацией моделируемых событий.
R+, с помощью которой в Е–сетях задаются значения времени выполнения переходов. Таким образом имитируются временные задержки, связанные с реализацией моделируемых событий.
Пятый элемент набора V = {Vs} задает непустое конечное множество переменных, количественных оценок состояния моделей.
Шестой элемент Q = {qm} описывает множество реализующих процедур, применяемых в Е–сетях для разрешения конфликтов на переходах и синхронизации событий.
Седьмой элемент – множество  ={
={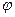 n} процедур переходов.
n} процедур переходов.
Восьмой элемент Мo= (Мo(Р1), ..., Mo(Р1p1)) обозначает начальную маркировку событий.
Каждый переход Е–сети имеет три характеристики и записывается как an= (
 ), где
), где  тип перехода; z
тип перехода; z 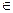 Z – время перехода;
Z – время перехода; 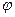 n – процедура перехода. Переход an
n – процедура перехода. Переход an 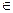 A выполняется в три этапа. Сначала проверяются условия активности перехода, а для Х – и У – переходов еще находятся значения решающей позиции и определяется конкретная схема срабатывания. На следующем этапе реализуется задержка выполнения перехода на время Zn и пересчитываются значения атрибутов метки по правилам, указанным в процедуре
A выполняется в три этапа. Сначала проверяются условия активности перехода, а для Х – и У – переходов еще находятся значения решающей позиции и определяется конкретная схема срабатывания. На следующем этапе реализуется задержка выполнения перехода на время Zn и пересчитываются значения атрибутов метки по правилам, указанным в процедуре На заключительном третьем этапе, в точном соответствии со схемой перехода, изменяются маркировки его входных и выходных позиций. Выполнение Е–сети регулируется решающими процедурами и процедурами переходов.
На заключительном третьем этапе, в точном соответствии со схемой перехода, изменяются маркировки его входных и выходных позиций. Выполнение Е–сети регулируется решающими процедурами и процедурами переходов.
Наиболее полный набор средств описания дискретных и дискретно–непрерывных систем в виде сетей событий применяются при построении Комби–сетей. Множество Р позиций Комби–сетей объединяют шесть подмножеств: Рэ – элементарные, Рт – с временной задержкой, Рд – долгоживущие, Рг – гибридные, Рк – коллективные и Рм – макропозиции. Каждой позиции сети отвечает некоторый характерный для данной позиции набор атрибутивных переменных (АТТR(Pi), Pi 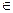 P). Позиции сети могут не иметь маркеров, иметь единственный маркер, накапливать маркеры (М:Р
P). Позиции сети могут не иметь маркеров, иметь единственный маркер, накапливать маркеры (М:Р N). При выполнении сети общее число действующих в ней маркеров изменяется и в каждый текущий момент времени равно МА. Все множество МА маркеров разбивается на четыре класса: булевские, с атрибутивными переменными, долгоживущие, изменяющие вид с элементарного на долгоживущие и обратно. С двумя первыми классами связаны элементарные маркировки (запрещены для позиций РД), третьему и четвертому классам соотносятся долгоживущие маркировки (запрещены для позиций Рэ, Рт, Рм). Каждый класс МК использует определенную структуру данных, все маркеры класса МК за исключением булевского класса имеют множество атрибутивных переменных АТТR (МК).
N). При выполнении сети общее число действующих в ней маркеров изменяется и в каждый текущий момент времени равно МА. Все множество МА маркеров разбивается на четыре класса: булевские, с атрибутивными переменными, долгоживущие, изменяющие вид с элементарного на долгоживущие и обратно. С двумя первыми классами связаны элементарные маркировки (запрещены для позиций РД), третьему и четвертому классам соотносятся долгоживущие маркировки (запрещены для позиций Рэ, Рт, Рм). Каждый класс МК использует определенную структуру данных, все маркеры класса МК за исключением булевского класса имеют множество атрибутивных переменных АТТR (МК).
Связи Е между позициями и переходами в Комби–сетях задаются обычным для сетей Петри способом:
Е 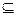 (Р х Т)
(Р х Т)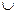 (Т х Р).
(Т х Р).
Подобно тому, как это уже имело место в рассмотренных нами расширениях сетей Петри, в ЕД–диаграммах также используется механизм разметки. Разметка выполняется отдельно для каждой компоненты диаграммы. Вершины–состояния компонент в каждый момент времени могут иметь или не иметь маркеров. Актуальные в текущий момент времени состояния маркируются.
Маркеры в вершинах компонент не накапливаются. Поскольку компоненты ЕД–диаграмм не имеют общих элементов, они не могут обмениваться своими маркерами. В любой момент времени в каждой компоненте диаграммы обязательно имеется хотя бы один маркер.
ЕД–диаграммы можно лишь условно отнести к расширениям сетей Петри. При их построении фактически использовался только механизм маркировки вершин, в некотором смысле аналогичный применяется в Е– и Комби–сетях.
Основное отличие ЕД–диаграммы от любых возможных расширений сетей Петри, ориентированных на имитацию, состоит в том, что в ЕД–диаграммах реализуется качественно иной принцип построения моделей, в основу которого положена идея описания систем в пространстве состояний.