Закон Гука для изотропных твердых тел
Основные закономерности поведения твердых тел в упругой области экспериментально впервые были изучены Р. Гуком. Им установлено, что при нагружении изотропного тела, когда деформации и напряжения достаточно малы, деформация пропорциональна приложенному напряжению (закон Гука):
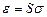 ,
,
где  – продольная деформация при растяжении;
– продольная деформация при растяжении;
S – константа упругой податливости, или просто податливость;
 – напряжения.
– напряжения.
Закон Гука можно записать и в такой форме:
 ,
,
где  – константа упругой жесткости, или просто жесткость.
– константа упругой жесткости, или просто жесткость.
В литературе, особенно технической,  часто называют модулем Юнга и обозначают
часто называют модулем Юнга и обозначают  , тогда
, тогда
 .
.
Закон Гука для сдвиговой деформации при действии касательных (скалывающих) напряжений имеет такой же простой вид, как и для случая растяжения:
 ,
,
где  – модуль сдвига (или модуль упругости при сдвиге);
– модуль сдвига (или модуль упругости при сдвиге);
 – тангенс угла сдвига.
– тангенс угла сдвига.
Закон Гука в приведенной выше форме определяет зависимость между напряжением и деформацией в одном и том же направлении, т. е. в направлении приложения внешней силы. Такая запись носит название элементарного закона Гука.
Однако деформация может возникать и в направлениях, отличных от направления приложения силы. В этих случаях закон Гука в элементарной форме уже недостаточен, и необходимо воспользоваться обобщенным законом Гука. В самом деле, при одноосном растяжении цилиндрического образца происходит не только его удлинение в направлении приложенной силы, но и сжатие образца в поперечных направлениях, т. е. имеет место трехмерная деформация. Поперечная деформация при упругом растяжении или сжатии характеризуется коэффициентом Пуассона  , равным отношению изменения размеров в поперечном направлении к их изменению в продольном направлении. Для большинства твердых тел значения
, равным отношению изменения размеров в поперечном направлении к их изменению в продольном направлении. Для большинства твердых тел значения  лежат между 0,25 и 0,35.
лежат между 0,25 и 0,35.
Обобщенный закон Гука устанавливает линейную зависимость не только между одним напряжением и соответствующей деформацией, а между всеми компонентами тензора напряжений и компонентами тензора деформации.
Обобщенный закон Гука для изотропного тела записывают
в следующем виде:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Константы упругости связаны между собой выражением
 .
.
Таким образом, зная две константы, можно всегда определить третью.