Моменты распределения
Одной из важных задач анализа рядов распределения является выявление закономерности распределения, определения ее характера и количественного выражения. Эта задача решается при помощи показателей, характеризующих форму, тип распределения.
Кроме рассмотренных выше важной характеристикой рядов распределения являются также моменты распределений.
Моментом распределения (Мк) называется средняя арифметическая из отклонений значений признака х от некоторой постоянной величины а в степени к. Порядок момента определяется величиной к. Эмпирический момент к-го порядка определяется по формуле
. В зависимости от постоянной величины а различают начальные, центральные и условные моменты. Если а = 0, то моменты называются начальными и определяются по формуле
;
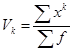В этом случае при к = 0 получим начальный момент нулевого порядка, который равен: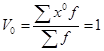 
. При к =1 получим начальный момент первого порядка, который равен: 
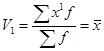, при к = 2 — начальный момент второго порядка, равный 
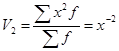, и т.д. Начальные моменты используются, в частности, при расчете дисперсии:
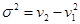,откуда 
.
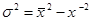Если постоянная величина а =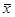 
, то получим центральные моменты, которые определяются по формуле 
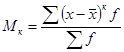. В этом случае при к = 0 получим центральный момент нулевого порядка, который равен: 
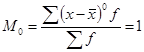, при к = 1 —центральный момент первого порядка, равный: 
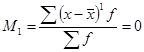, при к = 2 — центральный момент второго порядка, равный: 
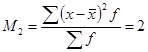, (дисперсии) и являющийся мерой колеблемости признака и т.д.
Если постоянная величина равна а, то моменты называются условными и определяются по формуле . В связи с тем, что вычисление центральных моментов, которыми довольно часто пользуются для характеристики рядов распределений, довольно громоздко, вначале вычисляют условные моменты, а затем по специальным формулам переходят от условных моментов к центральным. Так, математически доказано, что:
σ2 = m3 = M2-М12;
σ3 = m3 = M3 – М2 М1+ 2М12;
σ4 = m4 = M4 -4М3М2 +6М2 М12 - 3М13
Условные моменты используются для определения дисперсий высоких степеней σ2,σ4,σ3
Практически используются моменты первых четырех порядков. Если в качестве весов взять не частоты, а вероятности, то получим теоретические моменты распределения.