Метод моментов.

Точное решение стохастических уравнений является сложной математической задачей и зачастую невыполнимо. В этом случае может быть полезен метод моментов. Он состоит в том, что из уравнений (27) путем почленного умножения на N ⁿ и суммирования по N получают новые уравнения для моментов функции распределения.

(43)

Так, например, для рассмотренной выше бимолекулярной реакции 2А®В первые два уравнения для моментов функции распределения имеют вид

 

(44)

(45)

К сожалению, их структура такова, что производная по времени n-го момента определяется не только моментами более низкого порядка, но и (n+1)-моментом. Для расцепления этих уравнений необходимо выразить момент порядка (n+1) через моменты более низкого порядка. Например, если в уравнении (44) положить, что <N²> =<N>², то получим кинетическое уравнение, совпадающее с (25):

(46)

то есть уравнение так называемого модифицированного кинетического подхода.

Если в (44) положить <N ³> =<N ²> <N>, получаем систему двух уравнений относительно первого и второго моментов. Однако из-за нелинейного характера второго уравнения нельзя получить их решение в общем виде. Находя решения для первого момента из уравнения (46) и подставляя в (45), получим:

(47)

Существует также эмпирический подход для решения уравнений моментов (44, 45), в котором предполагается, что временная зависимость коэффициента вариации имеет вид

(48)

то есть связь между первым и вторым моментами задается некоторым параметром р

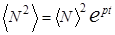(49)

Подставляя (49) в уравнение (44), находим его решение в виде:

(50)

Для определения параметра р поступим следующим образом. Продифференцируем уравнение (49)

(51)

и подставляя в (51) выражение для производной первого момента (44), получаем:

(52)

Приравнивая (52) и (45) при t=0, полагая при этом, что , получим

(53)

Для бимолекулярной химической реакции А+В®С, умножая уравнение (34) почленно на N и N₂ и производя суммирование по всем значениям N, получим следующие уравнения моментов для случая эквимолярного соотношения реагентов:

(54)

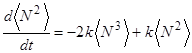(55)

Подставляя (49) в (54), получим следующее решение:

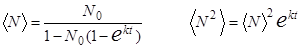(56)