Метод молекулярных орбиталей.

Метод молекулярных орбиталей (Гунд, Малликен , Хюккель, Герцберг) идеологически совпадает с методом Хартри –Фока, первоначально разработанным для атомов.

Каждый электрон имеет свою волновую функцию, имеющую вид произведения пространственной и спиновой функций ( спин - орбиталь) , полная волновая функция строится в виде детерминанта из одноэлектронных функций.

=.

 

Тогда уравнение для определения орбиталей и орбитальных энергий для синглетной конфигурации основного состояния имеет вид:

 

[=

 

 

 

 

 

Метод МО: -атомные орбитали. Рутан. Уравнение для коэффициентов разложения.

Волновые функции возбужденных состояний (конфигураций), возникающих при переходе между орбиталями i и k , тогда имеют вид:

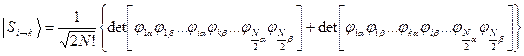
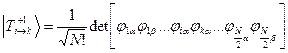
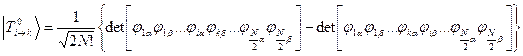
Энергии этих состояний равны

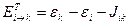
Правило Гунда для одной конфигурации .

 

 

 

 

 

 

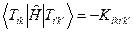
Виды МО: n, π, σ- связывающие π*, σ*- разрыхляющие.

 

Орбитальные типы состояний nπ*, ππ* σπ*, πσ*,nσ*,σσ*

 

S_ππ*, T_ππ* S_nπ* , T_nπ*

 

ΔE_ππ*(ST)~0,5-0,7эВ, ΔE_nπ*(ST)~0,1-0,2эВ

 

Зависимость энергии состояний от структуры молекулы.

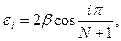
, ΔE_ππ*=

 

ΔE_nπ* =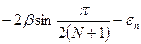

/

 

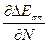Введение в молекулу электронодонорных заместителей ( ОН, NН₂) приводит к уменьшению энергии ππ*-состояний и некоторому увеличению энергии nπ*-состояний.

Образование водородной связи приводит к увеличению энергии связи n–электронов и увеличению энергии nπ* -состояний.

 

Метод ЛО

A-------B, A^--------B⁺, A*-------B, A-------B*