Вакуумная и плазменная электроника 4 страница

 

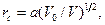(3.16)

где α=r₀/tgθ — расстояние от поверхности катода до плоскости кроссовера.

 

Из равенства (3.16) видно, что в первом приближении ра­диус кроссовера не зависит от площади эмиттирующей поверх­ности катода и определяется только отношением начальной энергии электронов (eV₀) к энергии электронов в области кроссовера (eV).

Выражение (3.16) было получено в предположении, что все эмиттируемые катодом электроны имеют одну и ту же началь­ную энергию (eV₀), в результате чего кроссовер обладает четко выраженной границей с радиусом r_c. Это предположение, од­нако, является слишком грубым, поскольку на самом деле элек­троны характеризуются максвелловским распределением по ско­ростям. Электроны с энергиями ниже(eV₀) пересекут плоскость кроссовера в точках внутри круга радиуса r_c, тогда как элек­троны с более высокими скоростями могут пересечь эту плос­кость при значениях радиуса, больших чем r_c. Каждая группа электронов с одинаковой начальной энергией попадает в круг определенных размеров в плоскости кроссовера, причем чем выше энергия электронов, тем больше радиус кроссовера. В слу­чае максвелловского распределения плотность электронов внутри кроссовера, не имея четко выраженной границы, будет быстро убывать по мере удаления от оси. Но этой причине ра­диус кроссовера обычно определяют как радиус круга, содер­жащего 90 % электронов.

Для того чтобы оцепить радиус кроссовера, необходимо знать распределение тока внутри кроссовера в зависимости от расстояния от оптической оси. В соответствии с максвеллов­ским распределением по энергиям число электронов (N), эмиттированных участком поверхности катода единичной площади в единицу времени в единицу телесного угла с начальными энергиями в интервале от eV₀ до e(V₀+dV₀), определяется соотношением:

 

(3.17)

 

где N₀ — число электронов, эмиттированных участком катода единичной площади в единицу времени и единичный телесный угол и имеющих произвольную энергию. Величину N_o можно выразить через плотность тока эмиссии катода (j_c), так как:

 

(3.18)

 

Ток, эмиттированный участком А в телесный угол от γ до γ+dγ, при энергиях электронов в диапазоне от eV₀ до e(V₀+dV₀), определяется формулой:

 

(3.19)

 

Этот ток течет через тонкое кольцо радиусом r (см. рис.3.6), причем плотность тока выражается следующим образом:

 

(3.20)

 

Рис.3.6. Корреляция между радиусом кроссовера и энергетическим разбро­сом.

 

Используя равенство (3.15) для вычисления r/dr, получаем:

 

(3.21)

 

Здесь V – потенциал в плоскости кроссовера. Соотношение (3.21) показывает, что в тонком кольце радиусом r = r_c плотность тока электронов, имеющих энергии от eV₀ до e(V₀+dV₀) не зависит от начального угла вылета эмиттированных элек­тронов γ.

Для вычисления величины полной плотности тока j(r) в плоскости кроссовера необходимо проинтегрировать плотность тока по всем тонким кольцам, соответствующим электронам с энер­гиями, большими чем eV₀, для которых выполняется условие r_c>r. Здесь предполагается, что все кроссоверы формируются в единственной плоскости, т. е. электронно-оптическая система источника не имеет хроматической аберрации. Интегрируя ра­венство (3.21), получаем следующее выражение для полной плотности тока в зависимости от радиуса:

 

(3.22)

 

где энергия eV₀ соответствует кроссоверу радиусом r. Используя максвелловское распределение по энергиям [равенства (3.17) и (3.16)], определяем:

 

(3.23)

 

 

или (3.24)

 

 

где j₀=(AN₀e/a²)(eV/kT) равно плотности тока в центре кроссовера; (r=0), а ρ₀²=a²kT/eV— постоянная величина для заданных условий работы источника электронов.

Плотность тока в центре кроссовера j₀ связана с плотностью тока эмиссии катода j_c, что приводит к ленгмюровскому пре­дельному соотношению:

 

(3.25)

 

Последнее получено из зависимости (3.24) заменой α² на r_c/tg²θ≈r₀²/sin²θ и с учетом того обстоятельства, что A=πr₀², а j_c=eπN₀ из равенства (3.18).

Из выражения (2.24) следует, что увеличение плотности тока в центре кроссовера может быть достигнуто за счет увели­чения плотности тока эмиссии катода (j_c) или уменьшения его рабочей температуры. Очевидно, что для термокатодов эти тре­бования противоречат друг другу, так как снижение темпера­туры катода всегда вызывает уменьшение плотности тока эмис­сии.

Для малых θ равенство (3.25) можно переписать в виде:

 

(3.26)

что идентично выражению (3.1). Это равенство имеет самый общий характер. При его выводе не накладывались никакие ограничения на конфигурацию полей или на устройство системы сжатия пучка.

Ленгмюровский предел (3.25) определяет максимальную тео­ретически возможную плотность тока, но это не значит, что та­кая плотность может быть реально достигнута. На практике хорошо спроектированные электронно-оптические системы позво­ляют получать величины максимальной плотности тока, состав­ляющие около 50 % от тех, которые следуют из ленгмюровского предельного соотношения.

 

Влияние пространственного заряда

 

Упрощенная теория формирования кроссовера основывается на предположении, что электростатическое поле в прикатодной области однозначно определяется потенциалами электродов источника электронов. Поле, создаваемое пространственным за­рядом электронов, не учитывается. Влиянием пространственного заряда можно пренебречь только для источников с малым первиансом Р, который определяется равенством:

 

(3.27)

 

где i измеряется в амперах, V—в вольтах. Внутреннее электрическое поле пучка оказывает заметное воздействие на движение электронов при P≥10^-3. Для пучков электронов, используемых в микролитографии, Р не превышает этой величины, и поэтому влияние пространственного заряда на формирование изображения не является существенным. Однако для ионных пучков, используемых для имплантации или отжига, влияние пространственного заряда необходимо учитывать.

Рис.3.7, а иллюстрирует образование трубчатого пучка из-за дрейфа электронов поперек ламинарных траекторий.

На рис.3.7,б показано, как образуется пучок с гауссовым распре­делением в том же трехэлектродном источнике при отсутствии влияния пространственного заряда. Видно, что действие пространственного заряда приводит к увеличению радиуса кроссовера и умёньшению тока в центре кроссовера.

 

а — трубчатый пучок; б — гауссов пучок.

 

Рис.3.7. Формирование пучка.

 

В прикатодной области, где скорость электронов мала, и вблизи кроссовера, где очень велика плотность тока, кулоновское взаимодействие между электронами намного больше, чем в области изображения. Это взаимодействие оказывает суще­ственное влияние на формирование пучка. Качественно наличие пространственного заряда в прикатодной области вызывает ра­диальный дрейф электронов поперек ламинарных траекторий и изменение распределения плотности тока.

 

3.4.Аберрации

 

На размеры и форму электронного пучка влияют также несо­вершенства электронно-оптических элементов, составляющих источник электронов.

Сферическая аберрация иммерсионного объектива (первой от катода линзы) влияет на формирование кроссовера. Ее воздей­ствие наблюдается даже при малых токах пучка, когда электроны отбираются только в центральной части катода. По мере увеличения тока (путем повышения температуры катода), когда электроны отбираются с больших участков поверхности катода и условия параксиальности нарушаются, становятся заметными другие разновидности аберраций. Из-за аберраций возрастание тока пучка сопровождается увеличением размеров кроссовера. Существуют четыре вида аберраций, характер­ных для электронных линз, которые используются в электрон­но-лучевых приборах.

 

Сферическая аберрация

 

Аберрации приводят к тому, что сечение пучка не может быть меньше предельного значения, называемого кружком наи­меньшего рассеяния (рис.3.8). В случае сферической абер­рации диаметр d_s этого кружка определяется пересечением не­скольких проходящих через линзу траекторий, которые не фо­кусируются в одной и той же точке на оси. Подобный дефект вызывается тем, что фокусирующие поля сильнее вблизи создающих их электродов, чем около оси. Диаметр кружка d_s наименьшего рассеяния определяется выражением:

 

(3.28)

где C_s – постоянная сферической аберрации, связанная с фокус­ным расстоянием f в параксиальном приближении: ;

K_s — константа, зависящая от геометрии линзы;

α—угол рас­ходимости пучка в области изображения (он может быть выра­жен через аналогичный угол в области объекта α₀ при помощи уравнения Лагранжа — Гельмгольца (3.11)).

 

Вносимую линзой сферическую аберрацию пучка нельзя скомпенсировать никакой последующей электронно-оптической системой. Поэтому при проектировании каждого электронно-оп­тического элемента необходимо добиваться наименьшей вели­чины C_s.

Действие этой аберрации на конечное изображение можно уменьшить за счет снижения тока пучка, устанавливая ограничивающую диафрагму внутри линзы, либо перед ней. Эта диа­фрагма уменьшает угол расходимости α фокусируемого пучка и тем самым влияние сферической аберрации. Уменьшение диа­метра пучка и увеличение плотности тока является частью за­дачи оптимизации при проектировании электронно-оптической системы.

Суммарная аберрация для двух линз, расположенных по­следовательно на расстоянии L друг от друга, с постоянными сферической аберрации C_s1 и C_s2 и фокусными расстояниями f₁ и f₂ может быть выражена через K_s=C_s/f следующим образом:

 

Рис.3.8. Сферическая аберрация.

 

Если вторая из линз много сильнее, т. е. f₁>>f₂, это выражение сводится к

 

(3.29)

 

Таким образом, аберрация более сильной линзы оказывает пре­обладающее влияние на аберрацию системы в целом.

 

Хроматическая аберрация

 

Хроматическая аберрация связана с чувствительностью фокусирующих свойств линзы к энергии частиц, пролетающих че­рез нее. Частица с более высокой энергией будет сфокусирована дальше от линзы, чем частица с меньшей энергией. Этот эффект проиллюстрирован на рис.3.8. Видно, что и в этом случае существует кружок наименьшего рассеяния, диаметр которого определяется соотношением:

 

(3.30)

 

где С_с—постоянная хроматической аберрации, часто записы­ваемая как С_с=K_сf, откуда видно, что хроматическая аберрация проявляется сильнее в линзах с большим фокусным расстоя­нием;

∆U— полный энергетический разброс.

 

Астигматизм

 

Астигматизм может появляться, если апертуры оптических элементов не обладают аксиальной симметрией, смещены или наклонены относительно оптической оси. Кружок наименьшего рассеяния характеризуется следующим равенством (рис.3.9, б):

 

(3.31)

 

Если апертура не является круговой, C_A определяется величи­ной δ, представляющей собой разность осей эллипса, описываю­щего форму апертуры: δ= α—b. Астигматизм можно скорректи­ровать, используя стигматор, простейший мультипольный эле­мент, в котором силовые линии электрического поля в области пучка имеют противоположные направления.

 

Дифракция

 

Частица пучка, пролетая через ограничивающую диафрагму, претерпевает дифракцию, в результате чего образуется пятно диаметром (рис.3.9, в)

 

(3.32)

 

 

 

 

 

α – хроматическая аберрация (d_c=C_c(∆U/U₀α)); б – астигматизм (d_A=C_Aα); в – дифракция (d_d=0,6λ/α).

 

Рис.3.9. Аберрация и дифракция.

Где λ—дебройлевская длина волны частицы, определяемая для электронов соотношением:

 

(3.33)

 

Размер кроссовера с учетом всевозможных аберраций обычно выражается среднеквадратичной суммой диаметров кружков наименьшего рассеяния:

 

(3.34)

 

В реальных условиях для трехэлектродного источника электро­нов существен только вклад от d_s, другие диаметры (d_c,d_A,d_d)обычно достаточно малы, и ими можно пренебречь.

 

Дефокусировка вследствие энергетического разброса в пучке

 

Энергетический разброс в электронном пучке определяется двумя факторами: температурой эмиттирующего катода и кулоновским взаимодействием электронов. Термический разброс сдвигает максвелловское распределение по энергиям в сторону больших значений, значительно увеличивает дисперсию, а также расширяет гауссовское распределение с увеличением плотности тока пучка. В настоящее время существует общее мнение, что этот эффект, впервые описанный Буршем, определяется главным образом электрон-электронным взаимодействием в рай­оне кроссовера, где плотность электронов максимальна.

Полный энергетический разброс в трехэлектродном источ­нике определяется выражением:

 

(3.35)

 

а для всего прибора:

 

(3.36)

 

Представление о физической основе этого эффекта можно по­лучить, рассматривая рис.3.10, где взаимодействие иллюстриру­ется геометрически. Предполагается, что опорный электрон летит вдоль оптической оси, а второй электрон — по произволь­ной траектории. Степень близости измеряется прицельным параметром b.

 

Рис.3.10. Схема кулоновского взаимодействия между электронами.

 

Рассматриваются три типа взаимодействия. Взаимодействие, параллельное b_z, т. е. вдоль оптической оси, приводит к измене­нию энергии. Рассеяние вдоль направления b_r вызывает смеще­ние траектории и, наконец, изменяется угол наклона траектории к оси α.

Были получены следующие результаты:

 

изменение энергии:

(3.37)

угловое смещение:

(3.38)

радиальное смещение:

(3.39)

здесь r_c—радиус кроссовера;

α₀— половинный угол расходимо­сти пучка в районе кроссовера;

V_b—энергия пучка (на единицу заряда);

λ определя­ется равенством:

 

(3.40)

где I_b – ток пучка.

 

Графики зависимости функций F₁,F₂ и F₃ от λr_c приведены на рис. 3.11. При больших токах все три функции стремятся к зави­симости от параметров типа (I_br_c/V_b)^1/2. При меньших токах графики более крутые и заметнее разли­чаются между собой. В ре­жиме сильных токов можно использовать соотношение между током пучка и ярко­стью β, чтобы исключить α₀ из равенства (3.37) и получить:

 

(3.41)

 

Этот результат был подтвержден экспериментально.

 

Рис.3.11. Графики зависимости F₁,F₂ и F₃ от λr_c.

 

Поскольку в электронно-оптических системах траекторию пучка можно рассматривать в виде последовательности кроссо­веров, а каждый кроссовер увеличивает энергетический разброс, для достижения минимальных размеров фокального пятна необходимо уменьшать их число. Кулоновское взаимодействие похоже на дифракцию в том смысле, что в отличие от других типов аберраций оно приводит к потере фокусирующей способно­сти системы, усиливающейся по мере уменьшения угла расходи­мости пучка.

В микротехнологических установках обычно не требуется достижение максимального разрешения, поэтому размеры фо­кального пятна можно сделать не оптимальными, увеличив ток. Связанные с аберрациями ограничения и возможности компро­миссов проиллюстрированы на рис.3.12 в виде графиков зави­симостей от угла расходимости пучка.

 

 

Рис.3.12. Зависимость ограничений на размеры фокального пятна от угла расходимости пучка (логарифмический масштаб).

 

В общем случае работо­способность системы ограничена сферической аберрацией. Для того чтобы увеличить ток пучка, необходимо увеличить апертурный угол до максимальной величины в соответствии с тре­буемым конечным размером изображения (d_i), который опре­деляется как:

 

(3.42)

Здесь d₀—уменьшенное изображение источника, d_s, d_c и d_d — характеристики соответствующих аберраций. В этом случае оп­тимальный результат достигается повышением тока на конечном пятне изображения за счет увеличения апертурного угла.

 

3.5. Устройство источников электронов

 

Для того чтобы вытягивать электроны из катода, ускорять их и получать требуемую конфигурацию пучка, необходима си­стема соответствующим образом спроектированных электродов. Эта система электродов должна создавать нужное распределе­ние электрических полей на поверхности катода и вдоль пути ускорения электронов. Часто именно ее и называют источником электронов.

Обобщенная модель трехэлектродного источника по­казана на рис.3.13. Электроны эмиттируются из небольшой об­ласти нити накала, прилегающей к оси. В непосредственной бли­зости от области эмиссии траектории электронов сильно искрив­лены, однако вскоре они спрямляются. Если экстраполировать траектории в противоположном направлении, то их пересечения будут соответствовать поверхности виртуального катода, кото­рый в общем случае не совпадает с реальным профилем эмиттирующей области нити накала. При проектировании трехэлек­тродного источника стараются обеспечить малые размеры именно виртуального катода.

Сеточный электрод Венельта и анод собирают ускоренные электроны в кроссовер или фокус внутри области, где существует электрическое поле, создаваемое электродами. Размер кроссовера определяется сферической аберрацией фокусирующей системы и размером виртуального катода. Обычно кроссовер имеет диаметр 10—50 мкм.

Количественно радиус виртуального катода определяется формулой:

 

(3.43)

 

где eV_k —кинетическая энергия электронов вблизи катода,r_h—радиус катода, V_ω—потенциал на оси в месте расположения цилиндра Венельта. Для вольфрамовой нити накала eV_k =0,25 эВ, а радиус виртуального катода:

 

(3.44)

 

Таким образом, радиус кроссовера можно записать в виде:

 

(3.45)

 

Рис.3.13. Модель Лауэра трехэлектродного источника.

 

Здесь V_A—потенциал анода; bz_A,z_ω—координаты положения, смысл которых ясен из рис.3.13.

Длиннофокусный источник (рис.3.14,а) проектируется та­ким образом, чтобы обеспечить фокусировку пучка на сравни­тельно большом расстоянии от анода. Такой эффект реализу­ется, если электрод Венельта имеет трубчатую форму и на него подано отрицательное напряжение смещения. В этом слу­чае силовые линии электрического поля катода расходятся, по­этому эмиттируемые электроны приобретают направленную от оси радиальную скорость. В промежутке между электродом и анодом эквипотенциали сначала становятся плоскими, а затем вытягиваются по направлению к аноду. В результате появля­ется направленная к оси радиальная составляющая скорости электрона, которая из-за более высокой энергии частиц имеет меньшую величину по сравнению с направленной от оси началь­ной радиальной составляющей скорости.

Благодаря этому пучок сходится довольно медленно и имеет большое фокусное расстоя­ние. Увеличение напряжения смещения приводит к росту фокус­ного расстояния за счет возрастания кривизны траекторий в прикатодной области и соответственно начальной расходимо­сти пучка, однако вызывает уменьшение тока пучка. Размер фо­кального пятна далее ограничивается током пучка, поскольку силы пространственного заряда действуют на увеличенной длине пути электронов.

В изображенном на рис.3.14,б градиентном источнике реа­лизовано послеускорение. Основным преимуществом такого ис­точника является то, что ток пучка не зависит от конечной энер­гии частиц V₅, потому что величина тока регулируется потен­циалом V₁ первой сетки. В результате появляется возможность варьирования полной мощностью пучка в широких пределах при очень малом изменении размеров фокального пятна. С дру­гой стороны, для этого требуются относительно большие на­пряжения. Для максимального использования преимущества такого источника необходимо, чтобы конечный потенциал V₅ был много больше V₁, который в свою очередь должен быть достаточно высоким для обеспечения нужной величины эмиссии с катода.

Вероятно, наибольшего прогресса в проектировании источни­ков электронов с большими значениями пространственного за­ряда достиг Пирс. Он разработал теорию и методику рас­чета, в соответствии с которой в последние десятилетия были созданы все источники с высокими плотностями тока. Для по­лучения ламинарных потоков частиц он предложил создать вблизи пучка такую конфигурацию электрического поля, кото­рая характерна для идеального диода. Пирс показал, что дей­ствие пространственного заряда внутри пучка электронов с ог­раниченными размерами может быть скомпенсировано специ­альным формирующим электродом, который создает вне пучка электрическое поле, удовлетворяющее необходимым условиям на границе пучка. Если эти граничные условия удовлетворя­ются, источник может рассчитываться так же, как и в случае потоков с пространственным зарядом, ограниченным в про­странстве между катодом и анодом идеального диода плоской, сферической или цилиндрической конфигурации (рис.3.14, в).

а— длиннофокусный источник; б — градиентный источник; в — поперечное сечение модифицированного тороидального источника Пирса.

 

Рис.3.14. Примеры схем источников электронов.

 

Плотность вытягиваемого тока в режиме эмиссии, ограни­ченной пространственным зарядом, при использовании плоскопараллельных электродов в диоде с межэлектродным расстоя­нием d и разностью потенциалов V, определяется законом Чайлда:

(3.46)

где V — в вольтах,

d — в сантиметрах.

 

Источник электронов Пирса рассчитывается так, чтобы обес­печить однородную плотность тока по поперечному сечению пучка. Для собирающих источников диаметр пучка становится минимальным на значительном расстоянии от анода, а за­тем пучок равномерно расходится. Основным достоинством ис­точника Пирса, кроме простоты расчета, является его высокая эффективность. Если предпринимаются разумные меры, она мо­жет достигнуть 99,9 % или более (т. е. менее 0,1 % катодного тока будет оседать на электродах источника).

 

3.6. Оптика источников электронов

 

Факторами, ограничивающими размер кроссовера и макси­мально достижимый в нем ток, являются яркость источника, аберрации линз, дифракция, изменение формы траекторий из-за действия пространственного заряда и увеличение энергетиче­ского разброса вследствие кулоновского взаимодействия. В общем случае эти факторы не могут быть исключены. Однако в разных источниках и для различных применений они могут меняться от пренебрежимо малых до ограничивающих работо­способность.

Из данных табл. 1 видно, что автоэлектронные источники по сравнению с термоэлектронными имеют очень высокую яркость. Однако такая яркость может быть достигнута только при очень малых размерах катодов и, следовательно, низком полном токе пучка. Вследствие этого преимущество высокой яркости авто­электронных источников по сравнению с обычными термоэлек­тронными реализуется только для пучков малых размеров (10— 100 нм), обычно характерных для электронной микроскопии.

В настоящее время оптические свойства автоэлектронных источников с точечными катодами подробно изучены. Можно отметить, что в них объектом служит не кроссовер, а виртуальный катод. Тогда размер пятна изображения (d) определяется аберрациями оптической си­стемы и допустимым углом расходимости. Другими словами, не размеры катодов определяют размер изображения, а ограничен­ная разрешающая способность набора линз оптической системы.

В случае термокатодов с «разрешимыми» размерами (d₀) размер пятна изображения (d) зависит от эффективного диа­метра кроссовера (d_i=2r_c) и аберраций линз оптической си­стемы. Эффективный размер кроссовера можно представить в виде:

 

(3.47)