В. Критерий Коши для функции.

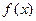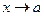Функция при , aÎD ( f )¢ имеет конечный предел тогда и только тогда, когда:

в которой .

Δ Необходимость. Пусть . Значит, .

Рассмотрим:

т.е. необходимость доказана.

Достаточность. Пусть .

Построим последовательность , такую что Î и . Для этой последовательности, по условию теоремы можно написать:

.

Тогда, согласно критерию Коши для последовательности , последовательность сходится и, значит (по Гейне ) функция имеет предел при . ▲