Краевые условия.

Уравнение (1.5) описывает процесс теплопроводности в самом общем виде, т.е. описывает целый класс явлений теплопроводности.

Пример: Пусть дано дифференциальное уравнение , его решение: , где С – постоянная интегрирования. Это набор прямых линий. Если уравнение 2-го порядка, то возникнут две постоянные и т.д. Для определенности решения нужно добавить краевые условия (КУ) или условия однозначности.

Определение.

КУ – это частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса. Следует различать условия однозначности:

1) геометрические –– должны быть заданы форма и размеры тела;

2) физические l, с, r, q_v(x,t) и др.

3) начальные (временные) если , то задается начальное распределение температуры .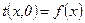

Часто принимают .

4) Граничные условия (ГУ) – характеризуют взаимодействие тела с окружающей средой.

Существует несколько способов задания граничных условий:

ГУ I pода - задано распределение температур на поверхности:

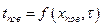, часто .

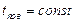ГУ II pода - задан тепловой поток на поверхности

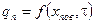; т.е. .

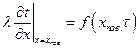Часто полагают 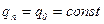. Например, первый период нагрева металла в нагревательных колодцах.

ГУ III pода - Заданы температура окружающей среды и закон теплообмена между средой и поверхностью тела. Чаще всего используется закон Ньютона-Рихмана:

q_пов=q_конв.,т.е. ,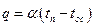

где a- коэффициент теплоотдачи Вт/м²К, характеризует интенсивность теплоотдачи между поверхностью тела и окружающей средой.

; .

Для высокотемпературных процессов должен учитываться нагрев тел излучением

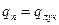или .

ГУ IV рода – когда заданы температуры и тепловые потоки в местах контакта двух разных тел:

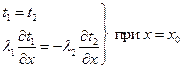Рис. 1.4. К граничным условиям четвертого рода

Дифференциальное уравнение совместно с условием однозначности дают полную математическую формулировку задачи теплопроводности, т.е. задачи нахождения температурного поля в твердом теле.

Эта задача может быть решена:

1) экспериментально; 2) теоретически.