Дифференциальное уравнение теплопроводности
При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности. Для сложных физических явлений, когда исходные величины могут существенно меняться в пространстве и времени на помощь приходит метод математической физики. Сущность метода: ограничивается отрезок времени от t до t+dt и из всего пространства V выделяется элементарно малый объём тела dV.
Вывод уравнения основывается на законе сохранения энергии или I-м законе термодинамики, записанного для dV и dt. Получим уравнение в декартовой системе координат, тогда 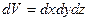 .
.
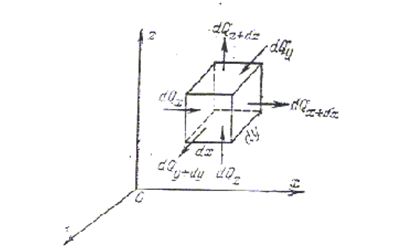
Рис. 1.3. К выводу диференциалоного уравнения теплопроводности
Полное количество теплоты, полученное телом
Q=cmΔt=cρVΔt или в дифференциальном виде dQ1=cρdVdT где Δt=tконечн-tнач=(t+dt)-t=dt. С другой стороны, используя понятие удельного теплового потока вдоль оси Х
dQ2=Dq×dF×dt, где ∆q=qx-(qx+dqx)=-dqх. Согласно закону сохранения энергии должно быть Q1=Q2 или тепловой баланс в дифференциальной форме: 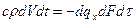 . Учтя, что
. Учтя, что 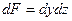 , разделив уравнение на dV и dt и используя закон Фурье:
, разделив уравнение на dV и dt и используя закон Фурье: 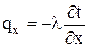 и т.д., получим
и т.д., получим
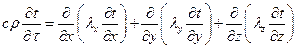 (1.5)
(1.5)
или в более компактном виде
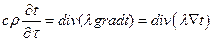 ,
,
где div – «дивергенция»- термин векторной алгебры
Если внутри тела действуют источники (стоки) теплоты, то в правую часть уравнений добавляется величина qV – объемная плотность внутренних тепловыделений (теплопоглощений)
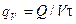 , Вт/м3.
, Вт/м3.