Биения.

Рассмотрим сложение колебаний одинаковой амплитуды и близких частот , , . Решение задачи усложняется.

.

Если изобразить эти колебания с помощью вектора амплитуды, то они вращаются с разными угловыми скоростями, и всегда будет момент, когда . Фазы в этот момент принимают за нуль. Тогда

.

= =

= .

=

- уравнение биений. Первый множитель медленно меняется, второй – быстро. Уравнение можно представить в виде

Сравним с уравнением гармонических колебаний

.

Уравнение биений – негармоническое, но меняется медленно, так как мало.

.

Поэтому биения – приблизительно гармонические колебания с медленно меняющейся амплитудой, может быть больше и меньше нуля.

- амплитуда. Для гармонических колебаний

- мало, велико. - частота биений.

 

 

Амплитуда ограничивает . (Проводим штрихами симметричную кривую внизу).Частота. . 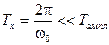Получили биения – усиление и ослабление колебаний.

Метод биений широко применяется на практике. Основан на сравнении искомой частоты с частотой эталона. Метод биений – это один из наиболее точных методов измерения частот, емкостей, индуктивностей. Применяют для настройки музыкальных инструментов.