Давление газа на стенку сосуда

При выводе уравнения состояния идеального газа будем считать молекулы маленькими твердыми шарами, заключенными в ящик объемом V (рис. 8.2). Предположение о твердых шарах означает, что между молекулами происходят упругие соударения. Рассмотрим сначала одну такую молекулу, отражающуюся от левой стенки ящика. Средняя сила, действующая на стенку на протяжении времени , равна

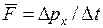. (8.9)

В результате соударения импульс изменяется на величину

. (8.10)

Поскольку время между соударениями молекулы с этой стенкой

, (8.11)

то на стенку со стороны одной молекулы действует средняя сила

. (8.12)

Рис. 8.2 Частица в сосуде объемом lS после отражения от левой стенки

Полная сила, с которой все N молекул в ящике действуют на стенку, дается выражением

, (8.13)

где – усредненный по всем частицам квадрат скорости .

Эта величина называется среднеквадратичной скоростью в направлении оси X. Разделив обе части этого соотношения на площадь стенки S, получим давление

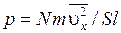. (8.14)

Заменим S l на объем V; тогда

, (8.15)

откуда

. (8.16)

Уже отсюда видно, что для данного количества газа произведение pV остается постоянным при условии, что кинетическая энергия частиц сохраняется без изменения. Правую часть формулы (8.16) можно записать через . Действительно,

.

Поскольку молекулы совершенно одинаково отражаются от всех шести граней, то

.

Тогда

, или .

Подставим теперь в (8.16) вместо величину :

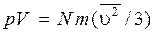. (8.17)

Мы будем определять абсолютную температуру как величину, прямо пропорциональную средней кинетической энергии молекул в сосуде:

(8.18)

(определение температуры), где – средняя кинетическая энергия, приходящаяся на одну частицу.

Коэффициент пропорциональности (2/3k) представляет собой константу. Значение постоянной k (постоянной Больцмана) зависит от выбора шкалы температуры. Один из способов выбора шкалы основан на том, что интервал температур между точками кипения и замерзания воды при нормальном давлении полагается равным 100 градусам (=100 К). Таким образом, величина k определяется путем измерения свойств воды. Экспериментально найдено, что

(8.19)

(постоянная Больцмана). Если с помощью (8.18) исключить величину 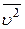из (8.17), то получим

. (8.20)

(уравнение состояния идеального газа).

Таким образом, применив уравнения ньютоновской механики к отдельным молекулам, т. е. использовав их на микроскопическом уровне, мы ввели важное соотношение между макроскопическими величинами p, V и T (ср. (8.20) с (8.7)).

Учитывая равенство (8.20), уравнение состояния идеального газа можно переписать в виде

, (8.21)

где n есть концентрация молекул. Так как для одноатомного газа средняя кинетическая энергия совпадает со средней энергией поступательного движения , уравнение (8.21) представим как

. (8.22)

Произведение дает суммарную энергию поступательного движения n молекул. Таким образом, давление равно двум третям энергии поступательного движения молекул, содержащихся в единице объема газа.