Концентрация свободных носителей

 

Для того, чтобы определить количество электронов в зоне проводимости, необходимо знать число уровней в зоне и вероятность их заполнения, учесть принцип Паули.

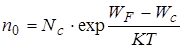или через потенциалы ,

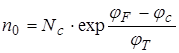где , , ,

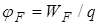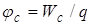– максимально возможная концентрация электронов для данной температуры в зоне проводимости или эффективная плотность состояний в зоне проводимости.

– граница (дно) зоны проводимости;

q – заряд электрона;

W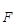– уровень Ферми.

В соответствии с теорией нахождение электрона на каком-либо уровне в полупроводнике определяется функцией распределения Ферми-Дирака

 

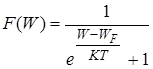или, если перейти к потенциалам, ,

 

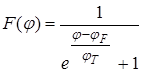где К – постоянная Больцмана, Т – абсолютная температура, – энергия или уровень Ферми,где – температурный потенциал, – потенциал Ферми, в принципе – это химический потенциал.

Формально, из функции распределения следует, что если , то . Т.о. это уровень, вероятность заполнения которого равна 1/2. Применительно к зонной структуре ПП функция распределения показана на рис. 2.8 для собственного ПП. Для электронов и для дырок, считая что дырка – это отсутствие электрона:

, .

 

Для большинства случаев в ПП и функция распределения Ферми-Дирака переходит в функцию распределения Максвелла-Больцмана

 

.

Оказалось, что уровень Ферми, его положение на зонной диаграмме строго соответствует концентрации свободных электронов и дырок. В собственном ПП он расположен близко к середине запрещенной зоны (к ), в электронном ПП у дна зоны проводимости (рис. 2.9а), в дырочном ПП – у потолка валентной зоны (рис. 2.9б). Например, если уровень Ферми совпадает с уровнем доноров, то это значит, что половина атомов примеси ионизована, а половина нет.

В акцепторном ПП , где – эффективная плотность состояний в валентной зоне.

В заключение следует отметить, что для данной температуры произведение – это закон действия масс.

Пример. Пусть для 300 °К см^-3. Это значит, что в донорном ПП с см^-3 содержится 10¹⁰ см^-3 дырок.