Интегрирование дифференциальных уравнений движения идеальной жидкости. Уравнение Бернулли для элементарной струйки идеальной жидкости

Перед тем, как начать интегрирование необходимо сделать ряд преобразований - умножить каждое уравнение соответственно на dx, dy, dz и просуммировать.

Используя те же соображения, что и при интегрировании дифференциальных уравнений равновесия жидкости

Учитывая, что

кроме того

Следовательно

Или окончательно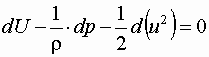

Полученное дифференциальное уравнение устанавливает взаимосвязь между силовой функцией, гидродинамическим давлением и скоростью в любом сечении элементарной струйки. Проинтегрировав, имеем .

Далее рассматривается частный случай, когда на жидкость из объемных сил действует только сила тяжести, следовательно

.

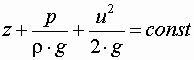Данное уравнение называется уравнением Бернулли для элементарной струйки идеальной жидкости.

Если рассмотреть два сечения, то можно записать

По аналогии с гидростатикой можно показать, что два первых слагаемых представляет собой удельную энергию: первое - удельную энергию положения; второе - удельную энергию гидродинамического трения. Третье - удельную кинетическую энергию. Сумма трех слагаемых является полной удельной энергией, т.е. напором.

С физической точки зрения уравнение Бернулли описывает частный случай закона сохранения энергии.

Геометрический смысл уравнения в том, что напорная плоскость горизонтальна.