СЛОЖЕНИЕ СКОРОСТЕЙ

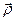Пусть точка М движется относительно подвижной системы координат. Получим теорему сложения скоростей. Для этого проведём векторы и 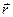, характеризующие по­ложение точки М относительно непо­движной и подвижной систем осей координат, и вектор точки О. Для любого момента времени

Продифференцируем по времени это векторное тождество, учитывая изме­нения векторов относительно непо­движных осей координат, т. е. вычис­лим полные производные. Получим

(1)

По определению, является абсолютной скоростью точки М, - абсолютной скоростью точки О. Для вычисления применим формулу Бура. Имеем

Относительная производная является относительной скоростью точки М по отношению к подвижной системе отсчета, а - угловая скорость вращения подвижной системы отсчета и, следовательно, радиуса-вектора 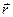, если бы он в рассматриваемый момент времени был скреплен с подвижной

системой осей координат. Таким образом, из (1) получаем

(2)

Скорость

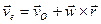
является скоростью точки свободного твердого тела, скреплен­ного с подвижной системой координат, с которой в данный момент совпадает точка М в движении тела относительно неподвижной системы осей координат. Это есть переносная

скорость точки М. Получаем следующую теорему сложения

(3) скоростей для точки:

т. е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.