УСКОРЕНИЯ ТОЧЕК ТЕЛА ПРИ ВРАЩЕНИИ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ

Формулу для ускорения какой-либо точки тела М можно получить путем дифференцирования по времени вектора скоро­сти, учитывая, что скорость вычисляют по формуле . Выполняя это дифференцирование, получаем

Так как

, ,

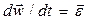то

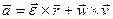(1)

Формулу (1) часто называют формулой Ривальса.

Часть общего ускорения точки

(2)

называют вращательным ускорением, а другую часть

(~)
- осестремительным ускорением. Следовательно, формула (1) примет вид

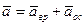
т. е. ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного.­

Модуль вращательного ускорения определяют аналогично модулю скорости v :

, (3)

где h₁ – кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение 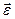(рис. 42).

Формула (3) для получается из (2):

,

где .

Модуль осестремительного ускорения можно получить из формулы (~):