СКОРОСТИ ТОЧЕК ТЕЛА ПРИ ВРАЩАТЕЛЬНОМ ДВИЖЕНИИ ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ

Скорость какой-либо точки М тела (рис. 41), по векторной формуле Эйлера,

(*)

Модуль скорости

где h-кратчайшее расстояние от рассматриваемой точки до мгновенной оси.

Таким образом, скорости точек тела пропорциональны расстояниям от этих точек до мгновенной оси. Направление скорости какой-либо точки тела перпендикулярно плоскости, в которой находятся векторы и 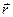, а следовательно, перпендикулярно отрезку h.

Если спроецировать правую и левую части (*) на координат­ные оси, то получим формулы Эйлера для проекций скоростей v_x, v_y и v_z:

; ; .

где х, у, z - координаты точек тела, скорости которых опре­деляются.

Если взять точки тела, лежащие на мгновенной оси, то получим следующие уравнения для координат этих точек:

; ; .

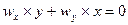Эти уравнения можно представить в виде

(**)

 

Если х, у, z являются текущими координатами точки мгновенной оси относительно подвижных осей, скрепленных с движущимся телом, а 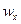, , 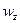проекции угловой скорости тела на эти оси, то формула (**) является уравнением подвижного аксоида.

Если взять подвижную систему координат Oxyz, скреплен­ную с телом, которое вращается вокруг неподвижной точки с угловой скоростью , то для единичных векторов , , , 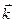направленных по этим осям координат, как для векторов, модули которых постоянны, имеем:

; ;

Эти формулы называют формулами Пуассона.