Метод простых итераций.
Пусть задано уравнение f(x)=0, где f(x) – непрерывная функция. Чтобы найти действительные корни этого уравнения, заменим его равносильным:
x=j(x). (4)
Теперь, чтобы решить уравнение (4) применяют метод последовательных приближений (метод итерации). Выбирают некоторое начальное приближение x0 и последовательно вычисляют следующие приближения:
xk=j(xk-1), k= 1.2,... (5)
Сходимость последовательности {хk} обеспечивается соответствующим выбором функции j (х) и начального приближения х0. Выбирая по-разному функцию j(х), можно составит разные итерационные методы решения уравнения (4).
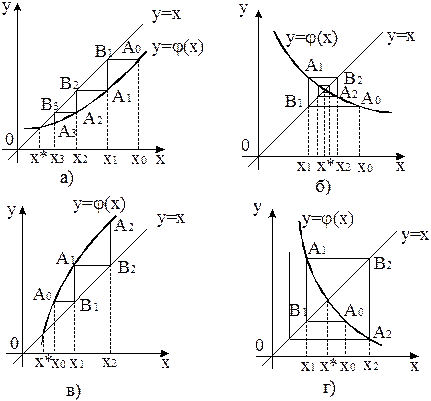
а) 0<’j (x) <1;
б)'-1<’j (x) <0;
в)j’ (x) >1;
г)j’ (x) <-1
Рисунок 1. – Геометрическое представление метода итераций
Метод итерации имеет простой геометрический смысл. Построим графики функцийу=х и у=j(х). Абсцисса точки сечения графиков этих функций является корнем уравнения (4) (рис. 1).
На отрезке [а; b] произвольно выбираем точкух0 и проводим через нее прямую, параллельную оси ординат до пересечения с кривой у=j(х)в точке A0 (x0, j(x0)). Из точки А0 проведем прямую, параллельную оси абсцисс, до пересечения с прямой y=x. В результате получим точку В1 с ординатой j(x0). Спроектировав точку B1 на ось Ох, находим абсциссу x1=j(x0). Аналогично через х1 проводим прямую, параллельную оси ординат, до пересечения с кривой у=j(х) в точке A1 (x1, j(x1)). Из точки А1 проводим прямую, параллельную оси абсцисс, до пересечения с прямой у=х в точке B2 (x2, j(x1)), абсцисса которой х2=j(х1) и т.д. В результате совместные абсциссы точек A1 и B1, A2 и B2 есть последовательными приближениями x1, x2, x3... корня х*.
Если |j' (х)|< 1, то последовательные приближения xk сходятся к корню х*, если |j' (х)|> 1, то последовательные приближения отдаляются от него.
Скорость сходимости зависит также от выбора начального приближения x0. Чем ближе к корню х* выбрано x0, тем быстрее будет найден результат.
Процесс итераций можно закончить, если будет выполнено следующее неравенство
|xk – xk-1|<e.