Решение.

КОНТРОЛЬНЫЕ ЗАДАНИЯ

ЗАДАНИЕ № 1.

1. Написать уравнение прямой, проходящей через точку M перпендикулярно плоскости a.

Координаты точек, уравнения прямых и плоскостей

.

M(1, - 2, 1), N(3, - 3, -1), K(4, 0, 3);

p: 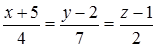, q: ;

a: , b: .

ЗАДАНИЕ № 2.

Даны матрицы A, B, C, D, H. Выполнить, если возможно, действия.

 

A–C, A+2D, AC, AD, BH

 

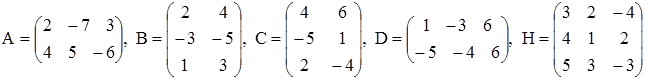
ЗАДАНИЕ №3

Исследовать и решить систему уравнений методом Гаусса

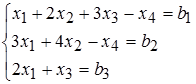
Вектор свободных членов b

 

 

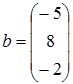
ПРИМЕРЫ РЕШЕНИЯ

Задание № 1.

ПРИМЕРЫ РЕШЕНИЯ

Задание № 1.

Вариант № 1.

Написать уравнение прямой, проходящей через точки M(2; 3;–1) и N(3; 2; 1).

Решение.

Каноническое уравнение прямой линии в пространстве имеет вид:

,

где – координаты любой точки, лежащей на прямой;

– координаты направляющего вектора прямой, т.е. координаты любого не нулевого вектора, параллельного прямой.

В качестве точки, лежащей на прямой, возьмем точку M(2; 3; –1), а качестве направляющего вектора прямой – вектор :

.

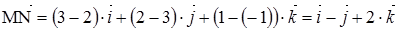Следовательно, уравнение прямой, проходящей через точки M и N, имеет вид:

.

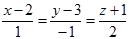Ответ: .

 

Вариант № 2.

Написать уравнение прямой, проходящей через точку M(2; 5; – 1) перпендикулярно плоскости a: 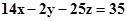.