Общие свойства стационарных состояний одномерного движения для дискретного спектра. Квантование энергии в потенциале притяжения. Осцилляционная теорема

Пусть потенциальная энергия частицы зависит только от координаты :

Тогда, поскольку потенциальная энергия не зависит от времени, волновые функции возможных состояний частицы описываются соотношением

(1)

где - произвольные числа, и - собственные значения и собственные функции оператора Гамильтона частицы (стационарного уравнения Шредингера):

(2)

Поэтому для построения всех решений временного уравнения Шредингера необходимо знать все решения стационарного уравнения Шредингера (2).

Так как потенциальная энергия зависит только от переменной , пространство вдоль осей и 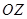однородно, вдоль них частица движется свободно, и такое движение можно описать с помощью плоской волны. В этом случае необходимо описать только ту часть волновой функции, которая зависит от координаты . Соответствующая часть гамильтониана имеет вид:

(3)

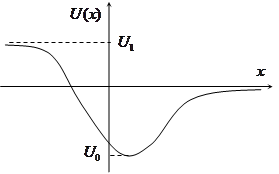Пусть потенциальная энергия частицы 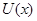является ограниченной функцией при всех конечных значениях координат. Также пусть функция 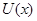стремится на бесконечностях к некоторым постоянным, одну из этих постоянных без ограничения общности можно выбрать равной нулю (изменяя начало отсчета энергий):

(4)

Докажем, что все собственные значения лежат выше уровня . Для этого возьмем произвольное состояние . Очевидно,

(5)

Поэтому

(6)

(так как среднее значение квадрата оператора импульса неотрицательно). Поскольку неравенство (6) выполнено для любого состояния , а для собственных состояний гамильтониана его среднее значение равно соответствующему собственному значению, то весь спектр лежит в области выше .

Докажем теперь, что при энергиях 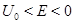могут существовать только дискретные собственные значения. Для этого рассмотрим асимптотику уравнения (3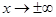) при . При 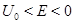асимптотики уравнения (3) имеют вид

(7)

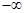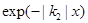где , . Как легко проверить, частными решениями уравнений (7) являются функции и на и и на . Это значит, что общее решение уравнения (3) содержит растущую и затухающую при 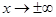экспоненты. Чтобы решение было конечным при 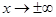, необходимо отбросить растущие решения, или, другими словами, наложить на решения два дополнительных условия: одно при , второе - при .

Поскольку уравнение (2) является дифференциальным уравнением второго порядка, его общее решение зависит от двух произвольных постоянных, причем одна из них всегда может быть выбрана как общий множитель, так как уравнение (2) однородно. Поэтому одновременно удовлетворить двум указанным граничным условиям, подбирая произвольные постоянные в общем решении, вообще говоря, невозможно. Действительно, так как одна из постоянных является множителем, то условия конечности решения при 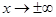могут дать только нулевое значение этой постоянной, то есть привести к тривиальному решению . Поэтому ненулевые ограниченные решения уравнения (2) при 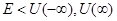, вообще говоря, не существуют. Однако, может оказаться, что при определенных значениях энергии некоторое ненулевое решение удовлетворяет обоим граничным условиям, при этом общий множитель в решении остается неопределенным (может оказаться, что таких значений не существует). Эти значения и будут собственными значениями оператора Гамильтона, а соответствующие ограниченные решения - собственными функциями. Таким образом, при 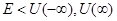спектр собственных значений (если они существуют) дискретен, а отвечающие этим собственным значениям собственные функции затухают при 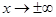. Из этих рассуждений также очевидно, что кратность вырождения дискретных собственных значений равна единице, то есть для каждого собственного значения существует единственная (с точностью до множителя) собственная функция. Собственные состояния оператора Гамильтона, отвечающие дискретному спектру, принято называть уровнями энергии.

Рассмотрим теперь уравнение (2) при . В этом случае асимптотика уравнения (2) при 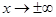также имеет вид (7), однако в области , а в области . Поэтому решениями уравнения (2) в области являются тригонометрические функции и , в области - растущая и затухающая экспоненты. Следовательно, при рассматриваемых значениях требования конечности накладывают только одно дополнительное условие на решения. Этому условию можно всегда удовлетворить, подбирая нужным образом одну из произвольных постоянных в общем решении дифференциального уравнения (2). Это значит, что в рассматриваемом случае для любого значения существует конечное решение уравнения Шредингера, причем на той бесконечности, где , это решение представляет собой линейную комбинацию тригонометрических функций и, следовательно, не затухает. Таким образом, любое число из интервала 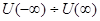является собственным значением гамильтониана, то есть спектр собственных значений непрерывен. При этом все эти собственные значения невырождены, поскольку общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные, одна из которых фиксируется условием конечности собственной функции на той бесконечности, где 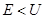, а вторая является множителем, который никак не может быть определен из уравнения, поскольку оно однородно.

Если выполнены оба неравенства , , то никаких ограничений на решение уравнения (2) требования конечности не накладывают, и ограниченные незатухающие решения существуют при любом значении величины . Очевидно, в этом случае собственные значения двукратно вырождены, так как дифференциальное уравнение второго порядка имеет два линейно независимых частных решения, а волновые функции собственных состояний остаются конечными при .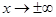

Сформулируем без доказательства одно важное свойство собственных функций оператора Гамильтона, относящихся к дискретному спектру, которое называется осцилляционной теоремой. Перенумеруем собственные значения одномерного гамильтониана в порядке их возрастания. Тогда собственному состоянию с минимальной энергией (основному состоянию) отвечает собственная функция, которая нигде не обращается в нуль (за исключением, может быть, границ доступной для движения частицы области), второму по энергии состоянию (первому возбужденному) - собственная функция, которая обращается в нуль один раз (или, как говорят, имеет один узел), второму возбужденному – функция с двумя узлами и т.д. Собственная функция -го по энергии состояния обращается в нуль (за исключением границ) 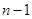раз, или имеет 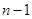узел.

Рассмотрим теперь вопрос о существовании собственных состояний дискретного спектра (из рассуждения, приведенных выше, следует только, что состояния дискретного спектра могут существовать только при энергиях, меньших граничных значений потенциала ).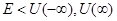

Рассмотрим сначала потенциал, обращающийся в нуль при 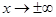, и пусть интеграл от функции 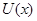отрицателен:

Возьмем волновую функцию , такую, что она нигде, кроме в ноль не обращается (гладкая и непрерывная вместе со своей первой производной). Обозначим за область, где волновая функция отлична от нуля. В этой области:

Поэтому

(8)

Из формулы (8) следует, что

и при больших : . Значит, существуют такие состояния, для которых средняя энергия отрицательна, а поскольку средняя энергия связана с собственными значениями и их вероятностями соотношением

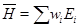(9)

из (9) заключаем, что , и, следовательно, условие - достаточное условие существования собственного состояния с отрицательной энергией, которое, поскольку потенциал обращается в нуль при 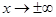, является состоянием дискретного спектра.

Остановимся теперь на интерпретации решений уравнения Шредингера. В случае дискретного спектра решения экспоненциально затухают при 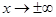, и, следовательно, во-первых, могут быть нормированы на единицу, а во-вторых, определяют такие состояния, в которых частица не уходит на бесконечность (поскольку вероятность обнаружить частицу на бесконечности стремится к нулю). Это значит, что такие волновые функции описывают движение частицы в ограниченной области пространства (финитное движение), или, другими словами, «связанное» потенциалом состояние частицы.

Совершенно другая ситуация имеет место в случае решений, отвечающих непрерывному спектру собственных значений. Эти решения не затухают при 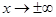и, следовательно, определяют состояния инфинитного движения.

Последний вопрос, который мы рассмотрим в этой лекции, это вопрос о четности решений стационарного уравнения Шредингера. Пусть потенциальная энергия - четная функция координаты. Тогда оператор четности 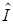коммутирует с оператором Гамильтона. Поэтому операторы и 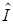имеют полную систему общих собственных функций, причем любая собственная функция одного из них, отвечающая невырожденному собственному значению, является собственной функцией другого. Поскольку все собственные значения оператора , отвечающие состояниям дискретного спектра, не вырождены, то соответствующие собственные функции оператора Гамильтона являются и собственными функциями оператора четности (то есть либо четными, либо нечетными функциями).

Из осцилляционной теоремы следует, что собственная функция, отвечающая связанному состоянию с минимальной энергией (его называют основным состоянием), с одной стороны, не имеет узлов, с другой - является либо четной, либо нечетной. Так как нечетная функция хотя бы один узел обязательно имеет (она обращается в нуль при ), то основному состоянию отвечает четная функция координат. Волновая функция следующего связанного состояния (которое называют первым возбужденным состоянием) обращается в нуль только один раз. Поэтому этот узел находится при (в противном случае существовал бы и второй нуль, симметричный относительно начала координат). А поскольку волновая функция в этой точке меняет знак (так как ее производная не равна нулю), то эта функция нечетная и т.д. Таким образом все собственные функции, отвечающие дискретному спектру, обладают определенной четностью, причем их четность чередуется в порядке возрастания энергии – четная-нечетная-четная-нечетная и т.д.

Состояния непрерывного спектра определенной четностью не обладают из-за двукратного вырождения. Однако из теоремы о коммутации операторов следует, что их можно выбрать так, чтобы они обладали определенной четность. При таком выборе для каждой энергии будут существовать четное и нечетное решения.

Если потенциальная энергия частицы не имеет определенной четности, то четных или нечетных решений уравнение Шредингера не имеет.