ВАРИАЦИОННЫЙ РЯД И ЕГО ПОСТРОЕНИЕ

При анализе совокупности часто полученные данные нужно сгруппировать и представить их в виде таблицы или ряда. При характеристике количественных признаков и большом числе ва­риант производят группировку данных и их разноску по классам, т. е. строят вариационный ряд.

Вариационный ряд — это упорядоченное изображе­ние реально существующего распределения особей в группе по величине признака. Вариационный ряд — это двойной ряд чисел, состоящий из обозначения классов и соответствующих частот. Он показывает, как изменяется признак от минимальной до максимальной величины, какая частота вариант в каждом классе. Класс, в котором встречается наибольшее число вариант, назы­вается модальным.

Для построения вариационного ряда необходимо: 1) из всей выборки (в нашем задании п = 64) найти максимальную (в дан­ном примере max = 11,4), минимальную (min = 3,2) варианты и разность между ними (max—min = 11,4—3,2 = 8,2); 2) опреде­лить число классов, которое зависит от объема выборки:

Число вариант Число классов

100-200 8—12

40-60 6-8

60-100 7-10

25-40 5-6

 

 

Найти классный промежуток (к) путем деления разности на предполагаемое число классов (к — 8,2: 8» 1,0); 3) установить начало классов, для чего к минимальному значе­нию признака 3,2 (лучше округленному в меньшую сторону до 3,0, но не больше, чем на величину к) прибавляют классный промежуток (к = 1,0), пока не включится максимальное значе­ние (11,4) признака (3,0; 4,0;... ;11,0); 4) установить верхние границы классов, которые должны быть меньше начала последу­ющих классов на величину, равную точности измерения призна­ка (3,0—3,9; 4,0—4,9;... ;11,0—11,9); 5) последовательно, начиная с первой, разнести варианты по классам (табл. 9).

9. Распределение сухостойных хорош черно-пестрой породы

Вершининского комплекса по количеству лейкоцитов н крови

(по данным П. Н. Ннконорова)

 

 

 

 

 

 

Показатель Шифр час­тот Число коров	Классы по количеству лейкоцитов в 1 мм1 крови (тыс.)	Всего 64
3,0-3,9	4,0-4,9	5,0-5.9	6,0-6.9	7,0-7,9	8,0-8,9	9.0-9.9	10,0— 10,9	11,0-П.9
1 1	2 4	Я П	4 Я Я	П	Г.	7 2	8 2	9 1

По вариационному ряду можно судить о распределении при­знака в данной группе. В крайних классах находится наименьшее число вариант, а в средних — большее. Причем видно смещение распределения вариант от середины вариационного ряда в сторо­ну больших значений классов. Наибольшее число вариант (48) относится к 3—5-му классам.

- Модальным классом (обладающим наибольшей час­тотой — 24) является 4-й класс (границы 6—6,9).

При рассмотрении вариационного ряда можно приблизитель­но определить среднее значение признака, находящееся между 6 и 6,9, вероятно, недалеко от 6,5, а также лимиты — 3,5—11,5 = 8 (взяты средние значения крайних классов). Среднее квадратичес-кое отклонение, исходя из лимита, равно 8 :6 = 1,3, потому что весь размах изменчивости охватывается шестью сигмами. Факти­чески полученные величины были близки к предсказанным х = 6,65; а — 1,51.

Графическое изображение вариационного ряда дает наглядное представление о характере распределения признака в изучаемой совокупности. Вариационный ряд можно представить в виде сту­пенчатой кривой, называемой гистограммой. Для этого на гори­зонтальной линии (ось абсцисс) наносятся классы, а на верти­кальной (ось ординат) — частоты. Основанием каждого столбика является соответствующее значение класса, а высотой — число

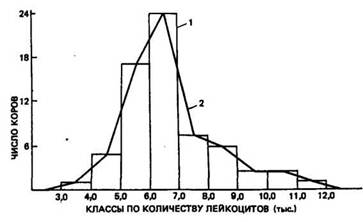
Рис. 31. Распределение коров по количеству лейкоцитов в 1 мм³ крови:

1 — гистограмма; 2 — полигон

особей в нем. Если соединить прямыми линиями середины всех столбиков, получается вариационная кривая, или полигон распре-деления. Полигон распределения своими ветвями должен касать­ся на' оси абсцисс середины соседних классов.

При анализе графика (рис. 31) можно видеть: 1) около сере­дины вариационной кривой располагается наибольшее число ва­риант; 2) распределение вариант по обе стороны от вершины вариационной кривой примерно симметрично; 3) число вариант (коров) убывает к краям вариационного ряда. Вышеназванные закономерности характерны для большинства вариационных рядов. Для сравнения на одном графике нескольких распределе­ний удобно пользоваться не гистограммой, а полигоном распре­деления.

Если взято малое количество животных, то в некоторых клас­сах вариационного ряда варианты могут отсутствовать, тогда ва­риационная кривая бывает разорванной. При малом числе осо­бей и растянутых вариационных рядах часто наблюдается д в у х -|§ершинность или многовершинность. Если выборка |Фаята достаточно большой, то двухвершинность указывает на ^смешение двух различных совокупностей (двух пород, линий и т. д.) или на выращивание и содержание животных в разных условиях и т. д.

Встречаются асимметричные вариационные кривые со смеще-|Нием влево или вправо, т. е: положительная или отри-|ц а т е л ь н а я асимметрия. Это объясняется неоднород­ностью условий развития животных данной совокупности, нали­чием в изучаемой группе большого количества особей с лучшими худшими наследственными задатками,, отбором. В нашем примере (см. рис. 31) наблюдается небольшая положительная асимметрия, т. е. вершина смещена влево. Если в средних клас­сах вариационного ряда наблюдается преобладание вариант, то получается островершинная кривая, называемая эксцессом.