Дифференциальные функции составляющих двумерной случайной величины

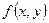Пусть дана двумерная случайная величина , заданная плотностью распределения и интегральной функцией . Согласно свойству 4 функции распределения двумерной случайной величины 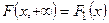; . Тогда, используя формулу (22.3), получим:

, .

Дифференцируя функции и соответственно по аргументам 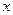и , получим плотности распределения вероятностей одномерных случайных величин Х и У:

,

.