Метод расстояний

В данном методе, помимо информации о показателях (х), коэффициентах сравнительной значимости показателей и характеристик направления действия показателей , требуется определить по имеющейся информации подразделение-эталон. Это реально не существующее подразделение характеризуется наилучшими значениями по каждому показателю среди всех имеющихся. Показатели подразделения-эталона 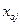строятся следующим образом:

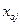= max 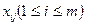при s_j = +1;

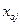= min 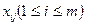при s_j = -1.

В каждом столбце матрицы Х находится наилучшее значение показателя; найденные значения образуют дополнительную строку чисел 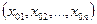- показателей подразделения-эталона.

Оценка R_i каждого i-ого подразделения вычисляется как квадрат расстояний между двумя точками в m-мерном пространстве, координаты первой – это значения показателей подразделения-эталона, а координаты второй – показатели подразделений i.

R_i вычисляется по формуле:

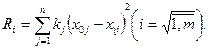(4)

Для вычисления «действительного» расстояния между точками m-мерного пространства необходимо извлечь квадратный корень из всех величин 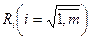, но, как правило, это действие не производится, поскольку оно не влияет на упорядоченность оценок.

Коэффициенты сравнительной значимости k_j необходимы для придания веса различным показателям в соответствии с их важностью. Чем больше k_j, тем более значим показатель j, тем в большей степени отклонение от эталона будет влиять на общую суммарную оценку R_i.

Критерий оценки наилучшего подразделения: min R_i (1im).

Метод расстояний наиболее формализованный из рассмотренных выше. Он легко позволяет учитывать значимость показателей, и его идея определения оценок как расстояний между точками-подразделениями и точкой-эталоном весьма убедительна.

Вместе с тем и этот методом имеет ряд недостатков:

1. Процедура вычислений сложна, а результаты не столь наглядны.

2. Сама по себе процедура оценки нуждается в совершенствовании: вариации различных показателей могут существенно отличаться, а это означает, что показатели с большей вариацией будут иметь больший вес в суммарной оценке, и, следовательно, неявно они получают преимущество по сравнению с другими показателями.

Сложность и не наглядность метода, возможно, и могут служить препятствием для его широкого применения, но в научных исследованиях на первый план выдвигаются требования обоснованности и логической непротиворечивости метода.