Преобразование агрегатного индекса. Средние гармонические и средние арифметические индексы.

Часто итоги по отдельным элементам сложного явления бывают несоизмеримы. Например, предприятие выпускает продукцию различного ассортимента. Если имеются данные о выпуске продукции только в натуральном выражении, то динамику выпуска нельзя нельзя охарактеризовать суммой индивидуальных индексов. Различные виды продукции не равнозначны по количеству затраченного на них общественного труда и имеют разные потребительские стоимости. Для получения общих итогов по предприятию необходимо данные по различным видам продукции привести к единой общей мере. Такой мерой чаще всего выступает стоимостная оценка. Для этого:

 

 

Мы ввели соизмеритель - цену единицы продукции данного вида. Общий индекс характеризует изменение объема производства при изменившихся ценах. Однако общий индекс не дает количественной оценки изменения объема выпуска продукции. Необходимо исключить влияние изменения цен на объем выпуска. Для этого количество продукции, произведенное в отчетный и базисный периодах необходимо умножить на одинаковые цены - агрегатный индекс физического объемаа - I_q.

В результате применения агрегатного индекса может быть получен итоговый показатель за период любой продолжительности. Поэтому можно изучать динамику выпуска не только отдельных видов продукции, но и по предприятию, отраслям промышленности в целом.

Общий индекс физического объема, построенны на базе индивидуальных индексов, принимает форму средних арифметических или средних гармонических индексов.

СРЕДНИЙ АРИФМЕТИЧЕСКИЙ ИНДЕКС

Пусть известна стоимость продукции каждого вида в базисном периоде

(p°q°) и известно значение индивидуального индекса физического объема

(i_q=q’/q°). Исходной базой для простроения среднего арифметического индекса является агрегатный индекс физического объема ()

I_{q средний арифметический}= S i_qd°

d° - удельный вес стоимости продукции одного вида в базисном периоде в общей стоимости всех видов продукции в базисном периоде.

I_{q средний арифметический} - применияется,если объем продукции отчетного пероиода неизвестен.

 

СРЕДНИЙ ГАРМОНИЧЕСКИЙ ИНДЕКС

ФИЗИЧЕСКОГО ОБЪЕМА

Пусть известны по каждому виду продукции стоимость продукции в отчетном периоде и индивидуальный индекс физического объема (Известно

q’p°, )

 

I_{q средний гармонический} =

По логической формуле средней из агрегатного индекса физического объема определяем средний гармонический индекс, то есть данный числитель делим на изветсный показатель - индивидуальный индекс физического объема. Если перечень изделий в текущем периоде не совпадает с их перечнем в базисном периоде, то нельзя определить индивидуальные индексы и преобразовать агрегатные индексы в средние.

 

ИНДЕКСЫ КАЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ

, q’=const

Индексы качественных показателей (себестоимости, цены, трудоемкости) рассматриваются в пересчете на объем производства (на количественную единицу).

Рассмотрим индексы качественных показателей на примере индекса себестоимости.

1. Для однородной продукции, выпускаемой на одном предприятии рассчитывается индивидуальный индекс себестоимости.

- либо в %, либо в коэффициентах

Чтобы узнать изменение себестоимости:

2. Определение общего изменения уровня себестоимости продукции разных видов, выпускаемых на одном предприятии: необходимо рассчитать агрегатный индекс себестоимости, то есть взвесить уровни качественного показателя z с помощью количества единиц продукции данного вида.

Агрегатный индекс себестоимости показывает, как изменяется уровень себестоимости в отчетном периоде по сравнению с базисным, если объем производства соответствовал уровню отчетного периода.

числитель - затраты отчетного периода

знаменатель - затраты приведенного к объему производства отчетного периода

Индексы цен:

1). индивидуальный индекс

2). для разнородных видов продукции одного предприятия расчитывают агрегатные индексы. Наиболее распространены:

- индекс Пааше:

q’ = const

- индекс Ласпейреса:

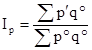
q°=const

Индекс Пааше применяется, если анализ проводится для определения экономического эффекта от изменения цен в отчетном периоде по сравнению с базисным. Он отражает разницу между фактической стоимостью продажи товаров в отчетном периоде и расчетной стоимостью продажи этих же товаров по базисным ценам.

Индекс Ласпейреса применяется, если целью анализа является определение товарооборота при продаже в предстоящем периоде такого же количества товаров, что и в базисном периоде, но по новым ценам. Этот индекс применяется при прогнозировании объема товарооборота в связи с намеченным изменением цен на товары в предстоящем периоде.

Средневзвешенные гармонические и арифметические индексы розничных цен и себестоимости определяется на основе преобразования агрегатного индекса.

Исходные данные - индивидуальный индекс или известное значение числителя и знаменателя.