Параметру

 

Изучение метода D - разбиения начнем с выяснения влияния на устойчивость одного параметра. При заданных значениях других параметров. Обозначим параметр символом . Это может быть коэффициент характеристического уравнения, или сочетание коэффициентов. Например, в уравнении

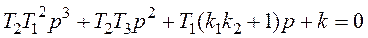
Можно назвать параметром T₁, T₂, T₃, k.

Допустим, сделан выбор l = T₂. Тогда уравнение примет вид

l(T₁²p³ + T₃p²) + T₁(k+1)p+k = 0 .

Полином, который умножается на l , обозначим Q(p), остальную часть S(p). Уравнение примет общий вид:

l Q(p) + S(p)=0 . (5.4)

Представив уравнение (5.4) в виде

, (5.5)

получаем как функцию переменной p.

 

Чтобы построить границы области устойчивости, полагаем

p = jw. Тогда l(p) становится комплексным числом:

l(jω) = -U(ω)+jV(ω) (5.6)

Если теперь задавать ω от 0 до +¥, вектор l(jω) вычертит некоторую кривую на комплексной плоскости U, V. Эта кривая отображает на плоскость U, V мнимую ось комплексной плоскости корней, то есть будет границей, по одну сторону которой k корней, по другую n - k.

Если задавать ω от 0 до -¥, получится зеркальное отображение кривой для +ω. Поэтому кривую рассчитывают для положительных ω, а затем дополняют зеркальным отображением относительно действительной оси.

 

Чтобы разобраться, по какую сторону находятся kкорней, область D - разбиения выделяется штриховкой. Соображения следующие.

При движении по мнимой оси в плоскости корней (рис. 5.23) от до та область, в которой находятся все корни устойчивости будет все время слева. Она показана штриховкой.

 

 

p

w ® +¥

V

Корни

устойчивости

 

w ® -¥