Определение длины и формы выравнивающего конуса аb

 

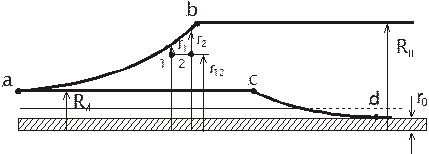Рис. 5.3.

 

Допустим, что диэлектрическая проницаемость одинакова.

Определим потенциал точки 1 и точки 2.

Разность потенциалов между токопроводящей жилой и точкой 1 определяется формулой:

;

.

 

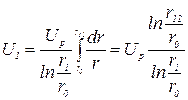Аналогично для точки 2:

.

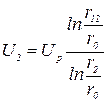Тогда:

;

.

 

Таким образом, потенциалы двух точек, лежащих на одинаковом расстоянии от жилы, но в разных сечениях не равны друг другу. Из этого следует, что в направлении оси кабеля появляется тангенциальная составляющая напряженности электрического поля. Эта напряженность будет максимальной у заземленного экрана, а на токопроводящей жиле она равна нулю.

 

Рис. 5.4.

Расчет геометрии выравнивающего конуса ведут исходя из условия, что тангенциальная напряженность на его поверхности постоянна и не превышает допустимого предела.

Для любой точки Р_х (рис. 5.4), находящейся на выравнивающем конусе, мы можем записать:

;

где E_px–радиальная напряженность в точке P_x.

Рассмотрим случай однородной изоляции, когда :

.

Подставим в формулу;

;

.

Введём новую переменную , тогда:

;

;

;

;

.

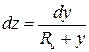Константу интегрирования С найдем из условий: x=0, y=0:

;

;

;

;

;

.

 

Пользуясь полученным выражением, мы можем найти профиль выравнивающего конуса.

На практике для расчета геометрии выравнивающего конуса берут не менее пяти значений r_x. Из этого же выражения мы можем получить длину выравнивающего конуса при r_x=R_п:

 

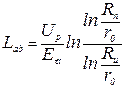; (1)

R_п – радиус подмотки.

 

Для случая неоднородной двухслойной изоляции ():

Рис. 5.5.

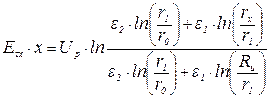; (2)

Для случая неоднородной трехслойной изоляции ():

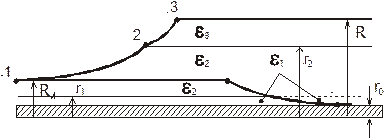
Рис. 5.6.

В этом случае расчет изоляции проводят двумя шагами:

1) вычисляют длину и форму выравнивающего конуса 12 (рис. 5.6) по формуле (2) для двухслойной изоляции;

2) вычисляют длину и форму выравнивающего конуса 23 (рис. 5.6) по формуле:

 

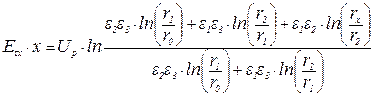; (3)

.