Понятие критерия разрушения
Важнейшим понятием механики разрушения является понятие критерия разрушения. Отметим различие задач теории упругости и механики разрушения. Если поставить и решить задачу теории упругости или пластичности для тела, имеющего тонкий разрез, то в полученное решение в виде параметра войдет размер разреза, как и иные размеры тела. При заданных и фиксированных внешних усилиях ряду значений длины разреза соответствует ряд значений компонентов напряженного и деформированного состояний. В полученном решении задачи теории упругости содержится длина разреза наравне с другими геометрическими размерами тела. Но при этом в нем не содержится связи внешнего усилия с длиной разреза при заданной нагрузке (при заданной нагрузке можно произвольно менять размеры тела, что отражается только на напряженно-деформированном состоянии). Для того чтобы получить такую связь, необходимо к полученному решению добавить некоторое условие или критерий разрушения, который переводит разрез в трещину. Такой критерий устанавливает величину усилия, при котором разрез начинает распространяться. В этом случае величина нагрузки и длина трещины становятся взаимосвязанными. При этом нельзя изменить длину трещины, не изменив и саму нагрузку. Если разрез получает возможность распространяться быстро или медленно, то такое состояние тела называют предельным или критическим, при этом критерий разрушения удовлетворяется.
Критерий разрушения устанавливает условие наступления предельного состояния равновесия. В состоянии предельного равновесия внешнее усилие и характерный размер трещины связаны функциональной зависимостью. Критерий разрушения является дополнительным уравнением к уравнениям теории упругости и пластичности. Поэтому наличие решений теории упругости для тел с тонкими разрезами еще не создает теорию трещин, в то же время основной вопрос теории трещин – установление и изучение критерия разрушения. Общий вид критерия разрушения
F(р,l) ≤ Fс, (2.18)
где F(р,l) – аналитическое выражение критериальной величины через параметр внешней нагрузки р и длину l трещины, а Fс – эта же величина, но найденная из эксперимента в критическом состоянии, при котором
F(pс,1с) = Fс. (2.19)
Величина Fс имеет смысл характеристики трещиностойкости материала. И сразу видно, что трещиностойкость материала может быть выражена через различные критериальные параметры механики разрушения F, входящие в левую часть выражения (2.18).
Можно показать, что силовой критерий разрушения эквивалентен энергетическому критерию Гриффитса.
В теле с симметричной трещиной длиной 2l при ее развитии в каждую сторону на величину δl освобождается упругая энергия –2(dW/dl)δl. Обозначив освободившуюся энергию –dW/dl на единицу площади через G, получим:
δГ=2Gδ. (2.20)
В выражении (2.20) величина G представляет собой приток энергии в вершину трещины, приходящийся на единицу площади трещины или, иначе говоря, интенсивность освобождающееся упругой энергии. Энергия Г обеспечивает существование тела как единого целого.
На образование новых поверхностей требуется энергия
δГ=4γδl,(2.21)
где, как и ранее, через γ обозначена поверхностная энергия, отнесенная к единице площади. Таким образом, из (2.20) и (2.21) имеем:
G=2γ, (2.22)
где G – механическая характеристика трещиностойкости материала, отражающая его сопротивление росту трещины и называемая вязкостью разрушения.
Поток энергии в вершину трещины при ее движении можно вычислить как работу, необходимую для «закрытия» трещины, исходя из следующих соображений.
Рис.2.4. Схематическое изображение конца трещины до ее продвижения на единицу длины (а) и после продвижения (б)
Представим себе мысленно, что на продолжении трещины (рис. 2.4 а) имеется разрез, на поверхности которого действуют напряжения, возникающие в зоне концентрации от воздействия внешней нагрузки. Тогда искомый поток энергии при продвижении трещины на единицу длины мысленного разреза, согласно схеме (рис. 2.4б) определится выражением
, (2.23)
где нормальное напряжение σу и перемещение v в случае плоской деформации берутся из формул (2.12) и (2.13) соответственно при θ=0 и θ=π (минус здесь стоит потому, что сила и путь, на котором сила совершает работу, направлены в разные стороны). При этом
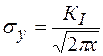, (2.24)
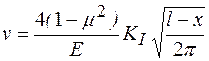. (2.25)
Подставляя (2.24) и (2.25) в (2.23) и производя интегрирование, получим
– для плоской деформации, (2.26)
– для плоского напряженного состояния. (2.27)
Итак, имеем две эквивалентные формулировки критерия разрушения:
1) энергетическую, согласно которой предполагается, что трещина может распространяться тогда, когда интенсивность освобождающейся энергии G достигает критического значения:
. (2.28)
2) силовую, согласно которой трещина может развиваться при достижении коэффициентом интенсивности К своей критической величины:
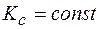. (2.29)
Эта эквивалентность вытекает из формул (2.26) и (2.27) для плоской деформации и плоского напряженного состояния соответственно:
, 
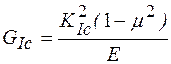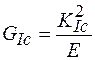. (2.30)
Формулы (2.30) справедливы для идеально хрупкого разрушения. В действительности, как указывалось, у большинства металлов в малой области вершины трещины из-за пластических деформаций проявляются нелинейные свойства материала. Однако вследствие малости области пластической деформации (где проявляются нелинейные эффекты) по сравнению с длиной трещины полагают, что размеры этой области и степень происходящей в ней пластической деформации контролируются коэффициентом интенсивности К и пределом текучести σ0,2. Поэтому для квазихрупкого разрушения оставляют в силе оба критерия разрушения Кс и Gc, полагая, что они зависят от характера сопротивления материала пластической деформации.
Итак, соотношения (2.28) и (2.29) в линейной механике разрушения являются основными. С их помощью можно рассчитывать предельные состояния элементов конструкций с трещиной, а также оценивать механические свойства материала и его способности тормозить развитие трещин.
В общем случае нагружения, когда возможны смещения берегов трещин относительно друг друга одновременно по трем рассмотренным схемам, получаем
–
для плоской деформации,
–
для плоского напряженного состояния.