Уравнение Бернулли для потока вязкой жидкости.

 

Рассмотрим участок трубы (в общем случае переменного сечения), по которому течет некоторая жидкость (рис. 7.37). Будем считать, что в пределах рассматриваемых поперечных сечений потока справедлив основной закон гидростатики, т.е. гидростатический напор в пределах сечения есть величина, одинаковая для всех точек данного сечения:

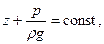
т.е. предполагаем, что при движении жидкости отдельные струйки оказывают одна на другую в поперечном направлении такое же давление, как слои жидкости в неподвижном состоянии. Это соответствует действительности и может быть доказано теоретически в том случае, когда течение в указанных поперечных сечениях является параллельноструйным (поэтому будем рассматривать именно такие поперечные сечения).

 

Введем понятие мощности потока. Мощностью потока в данном сечении будем называть полную энергию, которую проносит поток через это сечение в единицу времени. Так как в различных точках поперечного сечения потока частицы жидкости обладают различной энергией, вначале выразим элементарную мощность (мощность элементарной струйки) в виде произведения полной удельной энергии жидкости в данной точке на элементарный массовый расход:

Мощность всего потока найдем как интеграл от предыдущего выражения по всей площади :

Найдем среднее по сечению значение полной удельной энергии жидкости делением полной мощности потока на массовый расход. Принимая во внимание тот факт, что расход 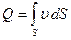, имеем:

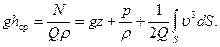
Умножив и разделив последний член на 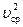, переходя к напорам, получим

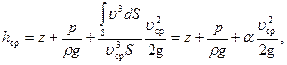(7.89)

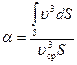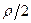где – безразмерный коэффициент Кориолиса, учитывающий неравномерность распределения скоростей в потоке. Если числитель и знаменатель выражения для умножить на , то станет ясно, что коэффициент Кориолиса представляет собой отношение действительной кинетической энергии потока в данном сечении к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.

Для обычного распределения скоростей (см. рис. 7.37) коэффициент всегда больше единицы, а при равномерном распределении скоростей равен единице.

Возьмем два сечения реального потока, первое и второе, и обозначим средние значения полного напора жидкости в этих сечениях соответственно и 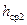. Тогда

(7.90)

где 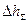– суммарная потеря полного напора на участке между рассматриваемыми сечениями.

На основе (7.89), выражение (7.90) перепишем в виде

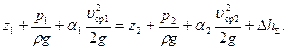(7.91)

Уравнение (7.91) представляет собой уравнение Бернулли для потока вязкой жидкости.

Как показывают опыты, во многих случаях гидравлические потери приблизительно пропорциональны квадрату скорости течения жидкости, поэтому можно принять, что в линейных единицах

,

или в единицах давления

.

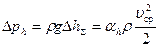Коэффициент пропорциональности называется коэффициентом потерь, или коэффициентом сопротивления.

Гидравлические потери обычно разделяют на местные потери и потери на трение по длине. Местные потери энергии обусловлены местными гидравлическими сопротивлениями (местными изменениями формы и размера русла), вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость, и обычно возникают крупные вихри. Потери на трение по длине – это потери энергии, возникающие в чистом виде в прямых трубах постоянного сечения и возрастающие пропорционально длине трубы. Рассматриваемые потери обусловлены внутренним трением в жидкости, а потому имеют место не только в шероховатых, но и в гладких трубах.

Рассмотрим для примера горизонтально расположенную трубку с постоянным сечением по длине, в которой течет некоторая жидкость. Тогда суммарная потеря полного напора 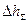между двумя сечениями, разделенными расстоянием , есть просто потеря на трение по длине. Представим коэффициент в виде

, (7.92)

т.е. свяжем его с относительной длиной участка трубки; 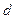– диаметр трубки. Тогда имеем

(7.93)

или в единицах давления

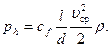(7.94)

Формулу (7.93) обычно называют формулой Вейсбаха – Дарси.

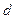Рассмотрим условие равномерного движения в трубке, т.е. равенство нулю суммы сил давления и трения в объеме, ограниченном длиной участка трубки и его диаметром . Это равенство имеет вид:

,

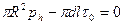где 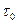– напряжение трения на стенке трубы (см. формулу (7.86’)).

Если учесть формулу (7.94), то легко получить

(7.95)