Структура двухслойной сигмоидальной нейронной сети

На рис. 4.2 представлена сеть с одним скрытым слоем. Все последующие рассуждения относятся к сетям именно такого типа. Обозначения сигналов и весов также будут соответствовать этому рисунку. Веса нейронов скрытого слоя пометим верхним индексом (1), а выходного слоя – верхним индексом (2). Выходные сигналы нейронов скрытого слоя обозначим 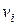(i=0, 1, 2,…, K), а выходного слоя (s=1, 2, …, M).

Пусть функция активации нейронов задана в сигмоидальной униполярной или биполярной форме. Для упрощения описания будем использовать расширенное обозначение входного вектора сети в виде , где 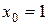соответствует единичному сигналу порогового элемента.

 

 

 

 

Рис. 4.2 Обобщенная структура двухслойной сигмоидальной нейронной сети

С вектором x связаны два выходных вектора сети: вектор фактических выходных сигналов и вектор ожидаемых выходных сигналов .

Цель обучения состоит в подборе таких значений весов и для двух слоев сети, чтобы при заданном входном векторе x получить на выходе значения сигналов , которые с требуемой точностью будут совпадать с ожидаемыми значениями для s=1, 2, …, M.

Если рассматривать единичный сигнал порогового элемента как один из компонентов входного вектора x, то веса пороговых элементов можно добавить в векторы весов соответствующих нейронов обоих слоев. При таком подходе выходной сигнал i-го нейрона скрытого слоя удается описать функцией

, (4.1)

в которой индекс 0 соответствует сигналу и весам пороговых элементов, причем , . В выходном слое s-ый нейрон вырабатывает выходной сигнал, определяемый как

. (4.2)

Из формулы (4.2) следует, что на значение выходного сигнала влияют веса обоих слоев, тогда как сигналы, вырабатываемые в скрытом слое, не зависят от весов выходного слоя.

Для того чтобы сеть можно было применять в дальнейшем, ее прежде надо обучить на полученных ранее данных, для которых известны и значения входных параметров, и правильные ответы на них. Это обучение состоит в подборе весов межнейронных связей, обеспечивающих наибольшую близость ответов сети к известным правильным ответам.

Определение числа промежуточных слоев и числа элементов в них является важным вопросом при конструировании многослойного персептрона.