Частотные характеристики.

При прохождении синусоидального сигнала через линейную цепь изменяются амплитуда и фаза сигнала. Причем эти изменения зависят от частоты входного сигнала. На рис.2 показано как синусоидальный сигнал проходит через линейную цепь. Свойство линейной цепи преобразовывать входной синусоидальный сигнал в зависимости от частоты описываются частотными характеристиками.

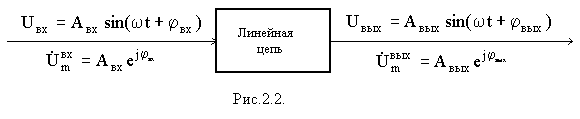
Различают две частотные характеристики:

- амплитудно-частотная характеристика (АЧХ);

- фазо-частотная характеристика (ФЧХ).

Амплитудно-частотная характеристика определяется как отношение амплитуды выходного сигнала к амплитуде выходного сигнала

А(ω) =А_вых/ A_вх.

АЧХ по существу представляет собой зависимость коэффициента усиления (передачи) цепи в зависимости от частоты входного сигнала

Фазо-частотная характеристика равна разности фазы выходного и входного сигналов

φ(ω) = φ_вых – φ_вх.

Зная частотные характеристики, мы всегда можем ответить на вопрос – чему равен выходной сигнал, если входной синусоидальный сигнал известен? Неизвестными величинами выходного сигнала являются амплитуда и фаза, которые можно найти из выражений

А_вых = A_вх·А(ω) и φ_вых = φ(ω) + φ_вх.

Для нахождения частотных характеристик используют метод комплексных амплитуд.

Перейдем к комплексным амплитудам. Пусть на входе действует сигнал , а на выходе . Найдем комплексный коэффициент передачи (усиления) цепи как отношения комплексных амплитуд выходного и входного сигналов

 

.

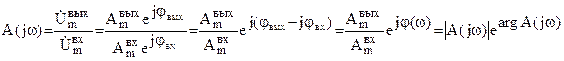Из полученного выражения видно, что комплексный коэффициент передачи содержит полную информацию о частотных свойствах цепи. Модуль комплексного коэффициента передачи представляет собой амплитудно-частотную функцию (характеристику), а аргумент – фазо-частотную функцию (характеристику). Комплексный коэффициент передачи находят методом комплексных амплитуд, который хорошо известен из курса ТОЭ.