Лекция 2

Определение приведенных моментов инерции масс звеньев машинного агрегата.

 

Машинный агрегат имеет структуру, которая представлена на рис. 3.

Одной из задач динамического синтеза является определение момента инерции маховика, обеспечивающего заданный коэффициент неравномерности установившегося движения δ.

Момент инерции маховика, установленного на валу ведущего звена исполнительного механизма, который является звеном приведения, определяется по формуле

,

где 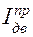– приведенный момент инерции ротора (якоря) электродвигателя, (1,1 – коэффициент, учитывающий приведенные массы муфт);

– приведенный момент инерции зубчатых колес и валов редуктора;

– приведенный момент инерции приводного механизма;

,

где – приращение кинетической энергии привода.

,

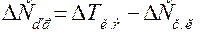где – приращение кинетической энергии машинного агрегата;

– приращение кинетической энергии звеньев исполнительного механизма.

В соответствии с уравнением работ

.

Приращение кинетической энергии звеньев исполнительного механизма определяется по формуле

,

где 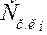– кинетическая энергия звеньев в i-м положении.

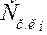– кинетическая энергия в начальном положении (минимальное значение).

где , _–_приведенный момент инерции звеньев исполнительного механизма в i-м и начальном положении, кг·м²;

ω₁ – угловая скорость звена приведения, 1/с.

 

Приведение моментов инерции звеньев исполнительного механизма.

 

По закону сохранения энергии кинетическая энергия приведенной массы (момента инерции) равна сумме кинетических энергий приводимых масс и моментов инерции.

.

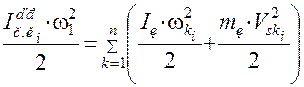Приведенный момент инерции звеньев исполнительного механизма в i-м положении

,

где 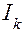– момент инерции k-го звена, кг·м²;

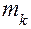– масса k-го звена, кг;

– угловая скорость k-го звена в i-м положении, 1/с;

– скорость центра тяжести k-го звена в i-м положении, м/с;

n – число подвижных звеньев.

По рассчитанным значениям и определяются величины приращения кинетической энергии звеньев исполнительного механизма

.

 

Определение приращения кинетической энергии машинного агрегата

 

По уравнению работ

,

где – работа движущих сил;

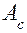– работа сил сопротивления.

где 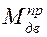– приведенный момент движущих сил;

– приведенный момент сил сопротивления;

– угол поворота звена приведения.

Приведенным моментом называется момент, приложенный к звену приведения, работа которого на элементарном угле поворота звена равна сумме работ приводимых сил и моментов.

Поскольку мощность – это работа в единицу времени, то мощность приведенного момента равна сумме мощностей приводимых сил и моментов.

Таким образом

.

,

где – момент, приложенный к i-му звену;

– угловая скорость i-го звена;

– сила, приложенная к i-му звену;

– скорость точки приложения силы P_i;

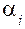– угол между векторами P_i и скорости V_i.