Решение линейных дифференциальных уравнений с постоянными коэффициентами операторным методом

Сущность этого метода состоит в том, что посредством интегрального преобразования от систем линейных дифференциальных уравнений переходят к вспомогательной системе алгебраических уравнений. Затем находят решение вспомогательной системы, а из него при помощи обратного преобразования получают решение исходной системы дифференциальных уравнений.

В качестве интегрального преобразования чаще всего используют преобразование Лапласа:

, (11.17)

где параметр p – некоторое комплексное число, y(t) – кусочно-непрерывная и ограниченная функция независимой переменной t, называемая оригиналом; Y(p) – изображение функции y(t). Помимо прямого преобразования существует обратное преобразование Лапласа, позволяющее по изображению Y(p) находить оригинал y(t). Сокращённое обозначение обратного преобразования: .

В курсах операционного исчисления приводят таблицы прямого и обратного пре-

образования основных функций.

Математическая операция	Оригинал	Изображение
Исходное преобразование	y(t)	Y(p)
Сложение оригинала
Умножение на постоянное число	аy(t)	аY(p)
Дифференцирование	dy/dt частн. случай: при y0=0	pY(p)-y0 pY(p)
n– кратное дифференцирование		PnY(p)-[pn-1y0+ +pn-2+…+]
Интегрирование
Сдвиг оригинала на (смещённый аргумент )	y(t -)

При анализе возмущенного движения ЛА часто возникает необходимость определить предельные значения решения дифференциального уравнения по виду этого уравнения, не решая его. Например, надо оценить поведение функции y(t) при t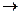0 или при t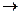, при условии, что система устойчива. Эту задачу решают при помощи следующих теорем о предельном переходе в преобразованиях Лапласа:

1. Если существует предел функции , то

(11.18)

2. Если существует предел функции , то

(11.19)